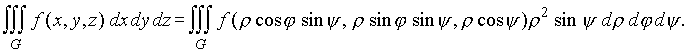|
|
|
|
|
|
||
3.7. Формула замены переменных в кратном интеграле.
Предположим, что G - ограниченная измеримая область в Rn , отображение
F: G
Rn взаимно однозначно и непрерывно дифференцируемо, область
G' =F(G) измерима. Пусть отображение F задается при помощи непрерывно дифференцируемых функций
Обозначим определитель матрицы частных производных этих функций - якобиан отображения F - через 
:
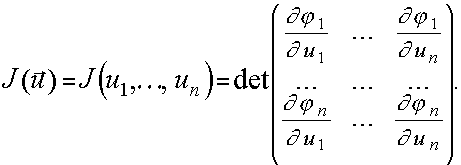
Кроме того предположим, что функция f ( 
) = f (x1 , . . . , xn) непрерывна на 
- замыкании области G.
Тогда справедлива формула замены переменных в кратном интеграле
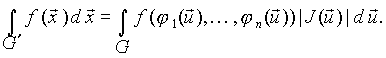
Опишем некоторые стандартные замены переменных.
Все вышеперечисленные требования выполнены при переходе к полярным, цилиндрическим или сферическим координатам (взаимная однозначность
отображений может быть нарушена на множестве нулевой меры - при 
,
что не влияет на соответствующий кратный интеграл).
осуществляет переход от полярных координат на плоскости к декартовым при помощи непрерывно дифференцируемых функций с якобианом
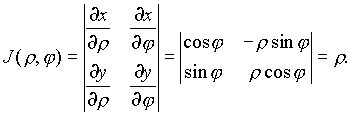
Формула замены переменных в двойном интеграле имеет вид
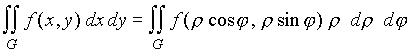
Для трехмерного пространства обычно рассматривают две стандартные системы координат - цилиндрическую и сферическую.
В стандартной цилиндрической системе координат в R3 на плоскости XOY
вводят полярную систему координат , а декартова координата z не изменяется. То есть, пусть в трехмерном пространстве задана прямоугольная декартова система координат и точка P имеет координаты (x, y, z) Зададим положение точки P' - проекции точки Р на плоскость XOY при помощи полярных координат ρ и φ , тогда положение точки Р в пространстве можно задать при помощи трех чисел (
, 
, z ), которые называют цилиндрическими координатами точки Р. Цилиндрические координаты связаны с декартовыми координатами следующими формулами:
, z = z .
Якобиан отображения , как и для полярных координат , равен :
.
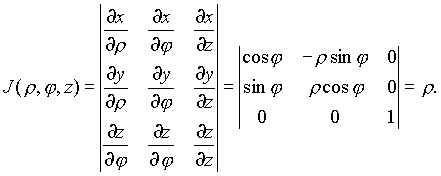
Формула замены переменных в тройном интеграле с переходом к цилиндрическим координатам имеет вид
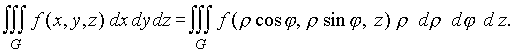
Для задания стандартных сферических координат снова зададим в трехмерном пространстве прямоугольную декартову систему координат. Пусть точка P имеет координаты (x, y, z). Зададим положение точки Р при помощи трех чисел ( , , 
) - сферических координат точки Р, где - расстояние от точки Р до начала координат, - полярный угол точки Р' - проекции точки Р на плоскость XOY, а - угол, который образует луч ОР с положительным направлением оси OZ ( угол измеряется от 0 до 
).
Сферические координаты связаны с декартовыми следующими формулами:
Якобиан преобразования имеет вид
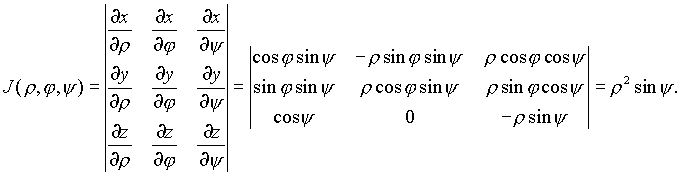
Формула замены переменных в тройном интеграле с переходом к сферическим координатам имеет вид
