Уровень: основной текст

Определение и свойства кратного интеграла Римана

3.1. Определение и свойства кратного интеграла Римана.

Пусть А - ограниченное n-мерное множество, имеющее конечный n-мерный объем

( _n (A) - при n = 2 - площадь, при n = 3 - объем, при n = 1 - длина, в общем случае мера Жордана). Разобьем множества А на k непересекающихся подмножеств : А₁ , А₂ ,...,А_k конечного обьема (если А - плоское множество, то множества А , А₁ ,

А₂ , ..., А_k имеют конечную площадь):

_n ( A_i ) < , i = 1,2,...,k.

Будем называть набор множеств T = { A_i }, i = 1, 2, ... ,k разбиением множества A.

Для каждого разбиения Т определим число l (Т) , называемое мелкостью разбиения:

обозначим через d (А_i ) максимальное расстояние между точками, лежащими в

множестве А_i или на границе множества А_i (то есть между точками замыкания

множества А_i). Число d (А_i ) будем называть диаметром множества А_i ; тогда мелкостью разбиения Т={ А₁ , А₂ ,...,A_k } назовем число :

Выберем в каждом множестве А_i точку М_i , i=1, 2, ... , k (точки М₁ ,...,М_k , называют точками пунктуации). Рассмотрим теперь функцию u = f(x₁ , x₂ ,...,x_n ) , ограниченную на множестве А.

Составим интегральную сумму :

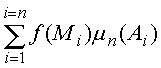Определение кратного интеграла - .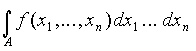

Число J назовем пределом интегральных сумм 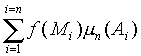при условии, что мелкость разбиения стремится к нулю ( I( T ) 0), если для любого числа

> 0 найдется такое число > 0, что для любого разбиения Т c мелкостью разбиения I( T ) < и любых точек пунктуации М₁, ... ,М_k выполнено неравенство

.

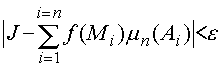Кратным интегралом Римана от функции u = f (x₁ , x₂ ,..., x_n ) по множеству А называется предел интегральных сумм при условии, что мелкость разбиения стремится к 0:

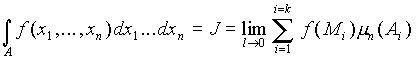
Если такой предел существует, то функция u = f ( x₁, x₂,... , x_n ) называется интегрируемой на множестве А.

Замечание.

Если А плоское множество (n = 2), то интеграл называется двойным интегралом, если А множество трехмерного пространства (n = 3), то

интеграл называется тройным интегралом. При этом используются обозначения

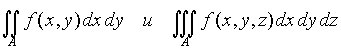
соответственно.

Утверждение.

1). Если функция u = f ( x₁, x₂,...,x_n) непрерывна на ограниченном , имеющем конечный n-мерный объем множестве А, то она является интегрируемой на А.

2). Ограниченная на описанном в пункте 1) множестве А, , функция

u = f( x₁, x₂,...,x_n) интегрируема на А, если n-мерный объем множества точек ее разрыва равен 0.

Например, если функция двух аргументов ограничена на квадрате и непрерывна во всех точках этого квадрата кроме точек, лежащих на каком-нибудь отрезке, то она интегрируема на квадрате, т.к. площадь отрезка равна 0.