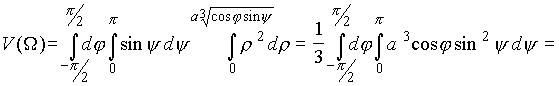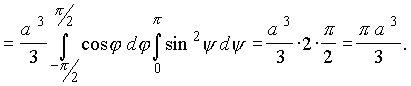Предыдущи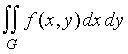й уровень изложения текущего раздела   Текущий уровень изложения предыдущего раздела   Текущий уровень изложения следующего раздела   Следующий уровень изложения текущего раздела   Уровень:


Формула замены переменной в кратном интеграле

Пример 1.

Перейти от - двойного интеграла в декартовых координатах по области G - единичному кругу с центром в начале координат к повторному интегралу в полярных координатах .



рис. 3.17





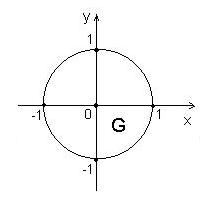
В полярных координатах аналогом прямых x=const, y =const являются окружности = const и лучи = const. Область G будет тогда задаваться как элементарная относительно (сравните с п.3.3 ) следующим образом:

.

Переходя к полярным координатам , имеем:





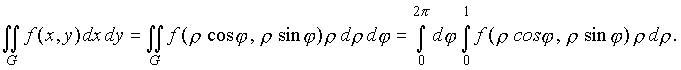
Пример 2. Перейти от 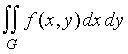- двойного интеграла в декартовых координатах по области G - единичному кругу с центром в точке ( 1, 0 ) к повторному интегралу в полярных координатах .



рис. 3.18





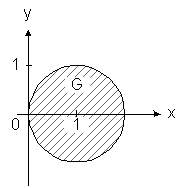
Уравнение окружности -- границы круга -- имеет вид (x - 1)2 + y2= 1

или x2+ y2= 2 x .

В полярных координатах уравнение этой окружности будет иметь вид

( cos )2+ ( sin )2= 2 cos или = 2 cos . Прямая x = 0 (ось OY) является касательной к рассматриваемой окружности, следовательно угол в рассматриваемой области G изменяется от (- /2 ) до

/ 2. На каждом луче = с, c (- /2 , /2 ) расстояние до начала координат для точек области G изменяется от 0 до наибольшего расстояния, соответствующего точке окружности и различного для разных лучей: = 2cos . Опишем область G как элементарную относительно (сравните с п.3.3 ):

Используя это представление области G, перейдем к повторному интегралу в полярной системе координат :



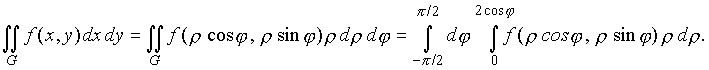
Замечание. Порядок интегрирования в полярной системе координат может быть и обратным. Например, в рассмотренном примере



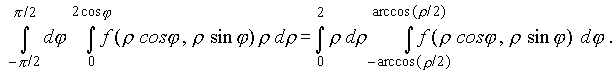
Пример 3. Перейти от 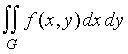- двойного интеграла в декартовых координатах по области G - единичному кругу с центром в точке ( 1, 1 ) к повторному интегралу в полярных координатах .



рис. 3.19





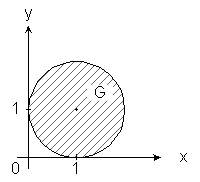
Уравнение окружности -- границы круга -- имеет вид (x - 1)2 + (y - 1 )2= 1.

Введем на плоскости новую систему декартовых координат -- новые оси координат параллельны осям OX и OY, точку О -- начало системы координат -- перенесем в точку (1, 1):

x' = x - 1, y' = y - 1

и рассмотрим стандартную полярную систему координат , соответствующую декартовой системе Х' ОY':

x' = cos , y' = sin .

Координаты (x , y) выразим через и

x = cos + 1, y = sin + 1.

Якобиан перехода от координат (х, у) к координатам ( , ), как и раньше, есть J ( , ) = , так как добавление константы не повлияет на производные.

В таких полярных координатах (полярная ось совпадает с прямой у = 1,

начало полярных координат в точке (1, 1)) уравнение окружности

(x - 1)2 + (y - 1)2 = 1 превращается в уравнение = 1 и, аналогично примеру 1 ,



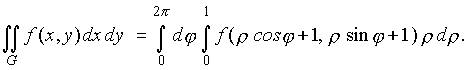
Пример 4. Преобразовать повторный интеграл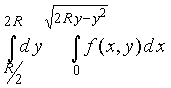

к полярным координатам .

Прежде всего найдем область интегрирования

G = { R / 2 y 2R , 0 x (2 R y - y2)1/2 }.



То есть у изменяется в полосе от R / 2 до 2R, при этом х изменяется от 0 до

правой полуокружности ( x 0 ) окружности x2 + ( y - R )2 = R2 . Таким образом наша фигура представляет собой полукруг без полусегмента.



рис. 3.20





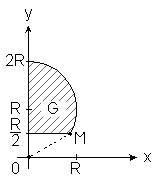
Найдем уравнения границ фигуры в стандартной полярной системе координат . Окружность x2 + (y - R)2 = R2 или x2 + y2 = 2R у будет задаваться уравнением = 2 R sin (это уравнение получается, если вместо x и y в уравнение окружности подставить их выражения через и ). Прямая y = R / 2 будет задаваться уравнением = R /(2 sin ).

Верхняя полуось OY соответствует значению = / 2. Область G заключена

между лучом ОМ и верхней полуосью OY. Луч ОМ соответствует минимальному значению полярного угла в области G, полуось OY - максимальному. Найдем угол, который образует с положительным направлением оси OX луч ОМ . Для этого

определим координату точки М, которая является пересечением прямой = R / (2 sin ) и окружности = 2 R sin . Следовательно, = 2 R sin = R / (2 sin ) в точке М.

Отсюда sin2 = 1/4, из того, что искомый угол принадлежит первой четверти, следует, что = / 6. На каждом из лучей, пересекающихся с областью G, координата минимальна для точки прямой = R /(2 sin ) и максимальна для точки окружности = 2 R sin . Из этих рассуждений получили описание области G как области, элементарной относительно переменной (сравните с п.3.3 ):



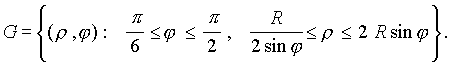
Теперь можно перейти по этой области к полярным координатам .



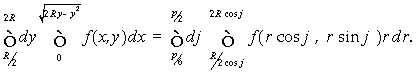
Пример 5. Вычислить интеграл 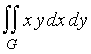, где G - область, ограниченная эллипсом x2/a2+ y2/b2 = 1 и лежащая в первом квадранте.



рис.3.21.





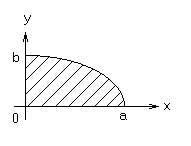
При интегрировании по эллипсу или его части удобно перейти к обобщенным

полярным координатам, положив

якобиан преобразования при этом будет J = ab .

Уравнение эллипса в обобщенных полярных координатах имеет вид =1, и наша задача преобразуется в следующую:

вычислить 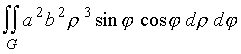, где G - область, ограниченная окружностью = 1 и лежащая в первом квадранте. Отсюда ( см. пример 1 ) имеем

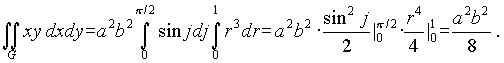
Пример 6. Найти полярный момент инерции для одного лепестка лемнискаты



(x2 + y2 )2= 2 a2(2 - y2).



рис. 3.22





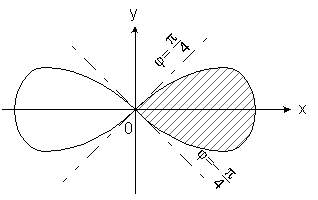
Полярное уравнение кривой 2 = 2a2 cos2 . Правый лепесток лемнискаты соответствует изменению полярного угла в пределах от - /4 до /4 .

Полярный момент инерции области G равен



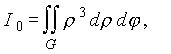
откуда имеем



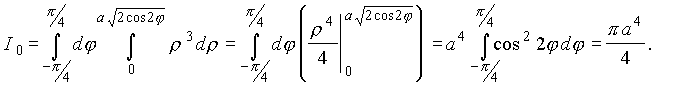
Пример 7. Вычислить объем тела, ограниченного поверхностями z = 0,

x2 + y2= x, z=2x2.. +2 y2..



рис. 3.23





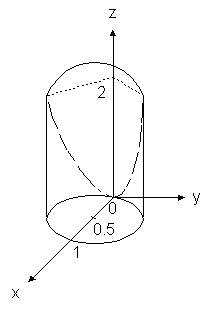
Заданное тело является цилиндрическим с образующей параллельной оси OZ, нижним основанием - кругом x2+ y2 x, лежащим в плоскости z = 0. Сверху тело ограничено параболоидом вращения z = 2 x2 +2y2. Следовательно, данное тело можно представить как область , элементарную относительно z :

где G - круг x2 + y2 x. Тогда объем V( ) равен (см. п.3.5 )

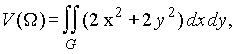
откуда, переходя к полярным координатам (см. пример 2 ), имеем



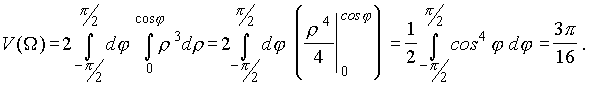
Пример 8. Вычислить объем тела, ограниченного сферой x2 + y2 + z2 = a2 и

прямым круговым цилиндром x2 + y2 a x.



рис. 3.24





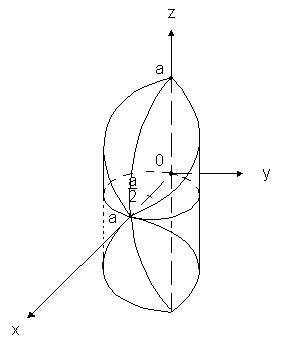
Данное тело является цилиндрическим с образующей параллельной оси OZ,

нижним основанием является часть полусферы z = - (a2 - x2 - y2 )1/2 , вырезаемая цилиндром x2 + y2 = a x, верхним - аналогичная часть полусферы z = (a2 ? x2 - y2)(1/2) . При переходе к цилиндрическим координатам тело можно представить как область :



Тогда объем V( ) равен (см. п.3.5 )

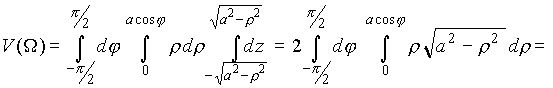
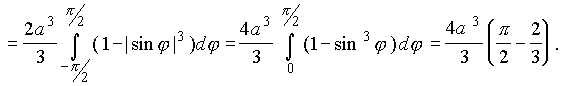
Пример 9. Вычислить объем тела, ограниченного параболоидом z = x2 + y2 и

плоскостью z = x + y .



рис. 3.25





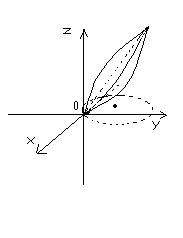
Найдем проекцию линии пересечения данных поверхностей на плоскость z = 0. Для этого исключим zиз уравнений z = x2 + y2 и z=x+y, получим

x2+ y2 = x + y - уравнение окружности, лежащей в плоскости z = 0, с центром в точке (1/2, 1/2) и радиусом R = 1 / 2(1/2). Перенесем начало декартовой системы координат в точку (1/2, 1/2, 0) и от новых декартовых координат перейдем к стандартным цилиндрическим :



Якобиан этого перехода J = . При переходе к этой системе координат тело можно представить как область , элементарную относительно z :

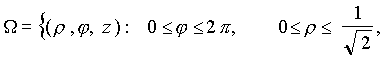
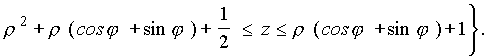
Используя это задание нашей области, найдем ее объем (см. п.3.5 )



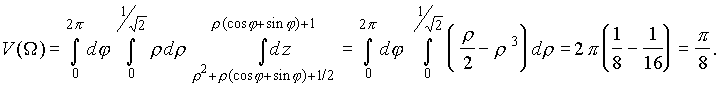
Пример 10. Найти объем тела, ограниченного сферой x2+ y2 + z2 = 2 и верхней половиной конуса z2 = x2+ y2.

рис. 3.26

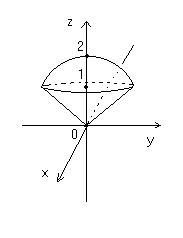
Проекция линии пересечения этих поверхностей на плоскость XOY имеет уравнение

x2 + y2 = 1 (линия пересечения этих поверхностей есть пересечение цилиндра

x2 + y2 = 1 и плоскости z= 1).

Перейдем к стандартным сферическим координатам

Якобиан преобразования имеет вид J = 2 sin . Уравнение заданной сферы в этих координатах имеет вид =2, уравнение полуконуса = /4, проекция тела на плоскость XOY есть круг, который задается неравенством

1.

Следовательно, тело можно описать следующим образом

Тогда объем заданного тела V( ) равен (см. п.3.5 )

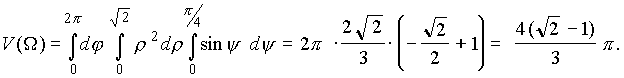
Пример 11 . Найти объем тела, ограниченного поверхностью

(x2+y2+ z2)2= a3x.

Заметим, что для данной поверхности переменная x 0. Как и в примере 10 , перейдем к стандартным сферическим координатам

Якобиан преобразования имеет вид J = 2 sin . Уравнение заданной поверхности в этих координатах имеет вид 3 = a3 сos sin . Угол может изменяться от 0 до , при этом sin положителен,

следовательно, сos положителен, откуда [- / 2, / 2 ] , при всех допустимых и изменяется от 0 до точки поверхности 3 = a3 сos sin . Отсюда имеем

Тогда объем заданного тела V( ) равен (см. п.3.5 )