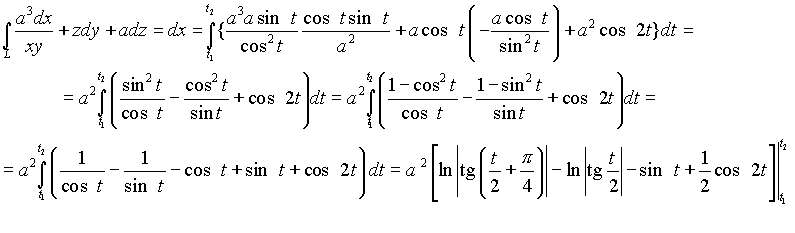|
|
|
|
|
|
||
Упражнения
1. Вычислить криволинейный интеграл второго типа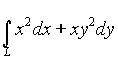 
,
где L - отрезок прямой от точки А (0, 1) до точки В (1, 2).
Уравнение прямой, проходящей через точки А и В, имеет вид 
, поэтому на отрезке АВ dy = dx.
Подставляя в подынтегральную функцию вместо у его выражение через 
и замечая, что при перемещении от А к В x меняется от 0 до 1,
по формуле (4.15) получаем
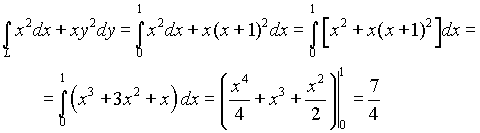
(см. упражнения )
2. Вычислить криволинейный интеграл второго типа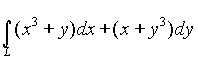 
,
где L - ломаная АВС (рис 4.7.), причем А(1,1), В(3,1), (3,5).
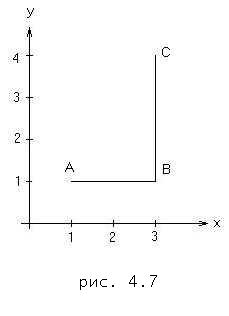
Так как контур интегрирования L состоит из отрезков АВ и ВС, то
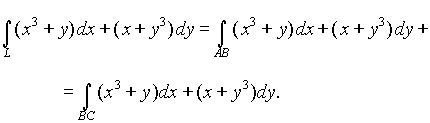
На отрезке АВ, уравнение которого 
; на отрезке ВС, уравнение которого 
, поэтому
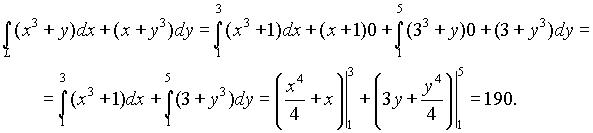
(см. упражнения )
3. Вычислить криволинейный интеграл второго типа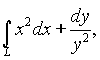 
где L - дуга кривой 
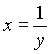от точки А(1,1) до точки В (4,1/4).
Линия L задана уравнением вида 
. В этом случае вместо формулы (4.15) целесообразно применить формулу
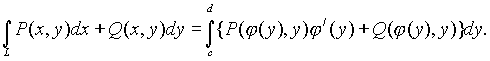
Поскольку в данном примере c=1, d=1/4,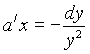 
, то
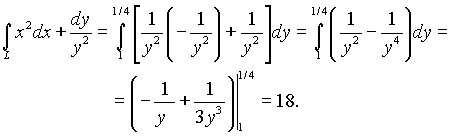
(см. упражнения )
4. Вычислить криволинейный интеграл второго типа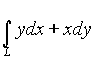 
, где L - дуга астроиды 
от точки 
до точки 
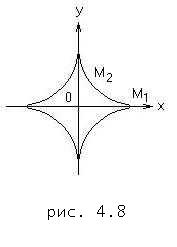
, для которых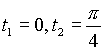 
(рис. 4.8)
Применим формулу (4.14), так как плоская кривая здесь задана параметрическими уравнениями. Из уравнений линии находим
Следовательно,
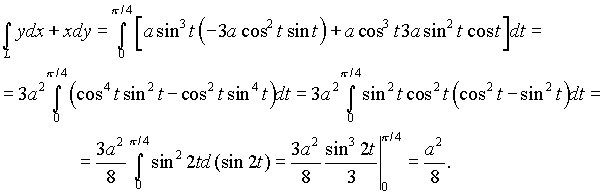
(см. упражнения )
5. Вычислить криволинейный интеграл второго типа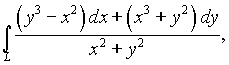 
где L - дуга окружности 
, пробегаемая в
направлении возрастания параметра t.
Замечая, что 
, по формуле (4.14) находим
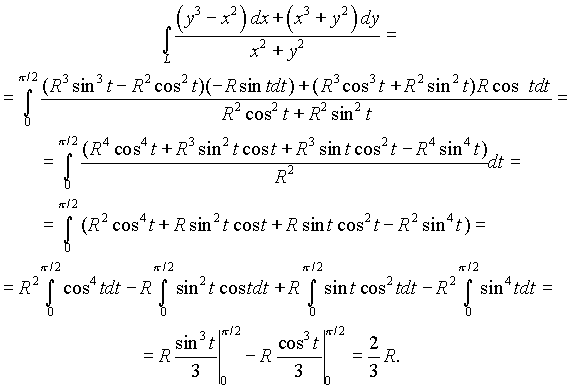
Замечание. Здесь принято во внимание, что
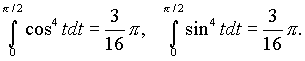
(см. упражнения )
6. Вычислить криволинейный интеграл второго типа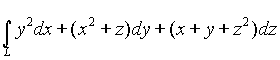 
,
где L - отрезок прямой в пространстве от точки А(1,0,2) до точки В(3,1,4).
Оставим уравнения прямой, проходящей через точки А и В :
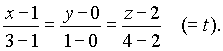
Из параметрических уравнений прямой
получаем
Из этих же уравнений видно, что при перемещении от точки А к точке В параметр t меняется от 0 до 1, т.е. пределы интегрирования в формуле (4.13), которой здесь нужно пользоваться, соответственно 
По формуле (4.13) находим
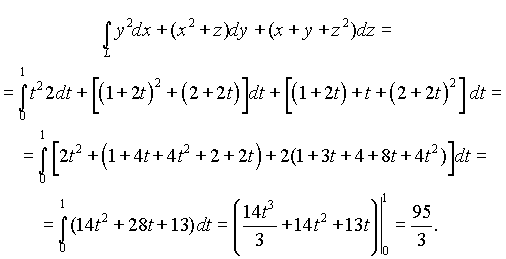
(см. упражнения )
7. Вычислить криволинейный интеграл второго типа
,
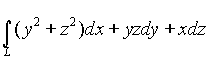где L - дуга винтовой линии 
Поскольку 
то
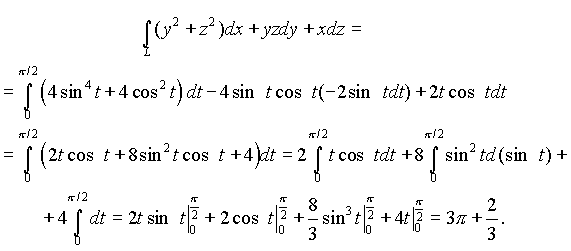
Замечание. Интеграл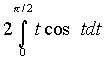 
вычислен с помощью метода интегрирования по частям:
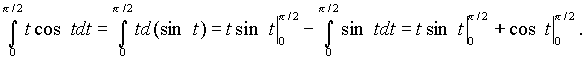
(см. упражнения )
8. Вычислить криволинейный интеграл второго типа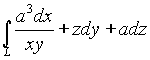 
, где L - дуга линии пересечения поверхностей 
.
Составим сначала параметрическое уравнение данной линии. Возведя в квадрат обе части первого уравнения, получим 
. Разделив почленно второе уравнение на , найдем
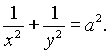
Из этого уравнения видно, что можно положить
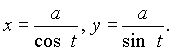
Из уравнения 
находим 
.
Итак, получены следующие параметрические уравнения линии:
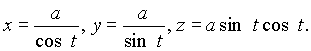
Принимая во внимание, что
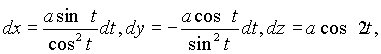
По формуле (4.13)
