1.3. Метод продолжений
1.3.1. Метод продолжений для полуограниченной струны
Рассмотрим задачу о распространении волн на полуограниченной прямой, (x≥0). Следует отметить, что чаще всего имеют дело со следующими способами закрепления струны:
При анализе этих задач нам понадобятся леммы о свойствах решений уравнений колебаний, определенных на бесконечной прямой.
Жесткое закрепление.
Задача ставится следующим образом:
ищем решение уравнения
  |
(1) |
удовлетворяющее однородному граничному
условию
U(0,t)=0
, t>0
и начальным условиям
 |
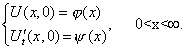(2') |
Рассмотрим функции Φ(x)
и Ψ(x) , являющиеся нечетными продолжениями функций φ(x)
и ψ(x), входящих в условие (2'):
 |
 |
Функция
определена для всех x и t >0. В силу леммы
1 U(0, t)=0.
Кроме того, эта функция удовлетворяет при t=0 и x>0
следующим начальным условиям:
 |
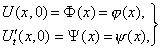x>0. |
мы
получим функцию, удовлетворяющую всем условиям поставленной задачи.Свободное закрепление.
Теперь рассмотрим случай, когда при x=0 мы имеем свободный
конец
.
Это значит, что касательная в точке 0 параллельна оси x (см. рисунок).
.
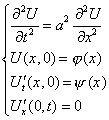Делаем четное продолжение функцийφ(x)
и ψ(x).
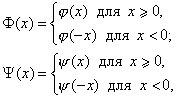
получим решение уравнения колебаний в виде функции
,
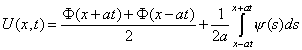определенной для всех x
и t >0. В силу леммы 2
.
Кроме того, эта функция удовлетворяет при t=0 и x>0
следующим начальным условиям:
| . |
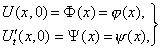Таким образом, рассматривая
полученную функцию U(x, t) только для мы
получим функцию, удовлетворяющую всем условиям поставленной задачи.
Вывод:
Для решения задачи на полуограниченной
прямой с граничным условием U(0,t)=0 начальные данные
надо продолжить на всю прямую нечетным образом.
Для решения задачи на полуограниченной прямой с граничным условием начальные
данные надо продолжить на всю прямую четным образом.