Леммы о свойствах решений уравнений колебаний, определенных на бесконечной прямой.

1. Если начальные данные в задаче о распространении колебаний на неограниченной прямой (задача (1)-(2)) являются нечетными функциями относительно некоторой точки , то соответствующее решение в этой точке равно нулю.

2. Если начальные данные в задаче о распространении колебаний на неограниченной прямой (задача (1)-(2)) являются четными функциями относительно некоторой точки , то производная по x соответствующего решения в этой точке равна нулю.

Доказательство леммы 1.

Примем за начало координат, =0. В этом случае условия нечетности начальных данных запишутся в виде

Функция U(x,t), определяемая формулой (9), при х=0 и t>0 равна

,

так как первое слагаемое равно нулю в силу нечетности φ(х), а второе равно нулю, поскольку интеграл от нечетной функции в пределах, симметричных относительно начала координат, всегда равен нулю.

Лемма 2 доказывается аналогично.

 

Условие четности начальных данных имеет вид

Заметим, что производная четной функции является функцией нечетной

.

Из формулы (9) следует:


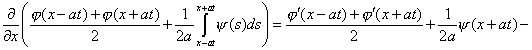
, t>0,

так как первое слагаемое равно нулю в силу нечетности ,
а второе – в силу четности .

Замечание:

Приведенное доказательство фактически опирается на формулу Даламбера и не связано с двукратной дифференцируемостью функции U(x,t). Тем самым доказано, что лемма 1 верна для любых функций, представимых формулой Даламбера, а лемма 2 – для функций того же вида с дифференцируемой функцией , то есть для обобщенных решений задачи (1) – (2).

 
<<назад