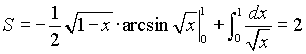|
|
|
|
|
||
2.6.1.а Решения
Требуемая площадь равна (см. п.2.6.1.а ) ![]() . Каждый из этих интегралов вычисляем по частям.
. Каждый из этих интегралов вычисляем по частям.
В первом принимаем ![]() . Тогда
. Тогда 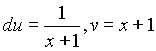 и
и
![]() .
.
Во втором интеграле положим ![]() . Тогда
. Тогда ![]() .
.
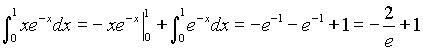
Складывая эти результаты, получим 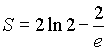 .
.
Искомая площадь равна (см. п.2.6.1.а ) 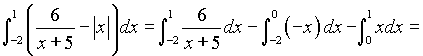
=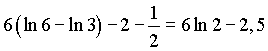
Решая систему 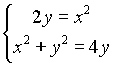 , получим координаты точек пересечения данных кривых: (0,0), (2,2) и (-2,2).
, получим координаты точек пересечения данных кривых: (0,0), (2,2) и (-2,2).
Преобразуем уравнение окружности к каноническому виду ![]() , откуда выразим y:
, откуда выразим y: ![]() . Так как по условию задачи нам нужна верхняя часть окружности, то берем ветку со знаком +.
. Так как по условию задачи нам нужна верхняя часть окружности, то берем ветку со знаком +.
Тогда площадь между кривыми вычисляется по формуле п.2.6.1.а . Учитывая симметрию области, получим:
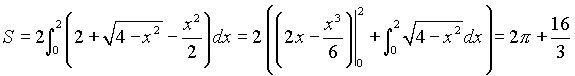
Рассматривая соотношение ![]() как функцию x от аргумента y, построим график этой функции
как функцию x от аргумента y, построим график этой функции
Интеграл тоже будем считать по переменной y:
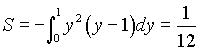
Решая систему уравнений 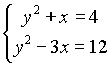 , получим точки пересечения данных парабол
, получим точки пересечения данных парабол ![]() . Интеграл удобнее считать по переменной y, поэтому, выразив из этих уравнений x и учитывая симметрию области, получим
. Интеграл удобнее считать по переменной y, поэтому, выразив из этих уравнений x и учитывая симметрию области, получим
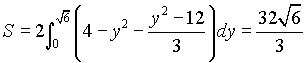
Решая систему уравнений 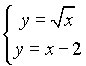 , получим точку пересечения данных кривых (4,2). Тогда искомая площадь будет равна (см. п.2.6.1.а )
, получим точку пересечения данных кривых (4,2). Тогда искомая площадь будет равна (см. п.2.6.1.а )
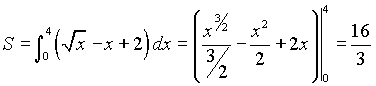
Производная ![]() от данной функции в точке
от данной функции в точке ![]() будет равна 4. Поэтому, подставляя в уравнение касательной
будет равна 4. Поэтому, подставляя в уравнение касательной ![]() данные задачи, получим уравнение требуемой касательной y=4x-6. Искомую площадь будем искать как разность площадей криволинейной трапеции под заданной кривой на промежутке [0,3] и площади треугольника, лежащего под касательной на промежутке [3/2,3].
данные задачи, получим уравнение требуемой касательной y=4x-6. Искомую площадь будем искать как разность площадей криволинейной трапеции под заданной кривой на промежутке [0,3] и площади треугольника, лежащего под касательной на промежутке [3/2,3]. ![]()
Искомая площадь вычисляется с помощью несобственного интеграла 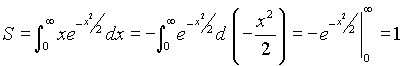
Очевидно, что искомая площадь вычисляется с помощью несобственного интеграла : 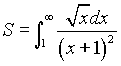 , который мы будем вычислять сначала с помощью подстановки
, который мы будем вычислять сначала с помощью подстановки ![]() . Тогда
. Тогда 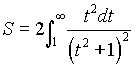 . Последний интеграл возьмем по частям, положив
. Последний интеграл возьмем по частям, положив  . Отсюда
. Отсюда 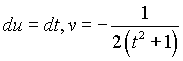 и
и 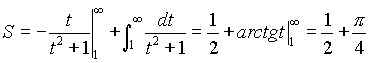
Искомая площадь вычисляется с помощью несобственного интеграла от неограниченной функции : 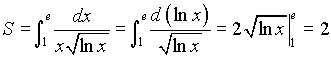
Искомая площадь вычисляется с помощью несобственного интеграла от неограниченной функции 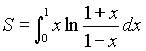 . Найдем первообразную подынтегральной функции, которую вычислим по частям, положив
. Найдем первообразную подынтегральной функции, которую вычислим по частям, положив 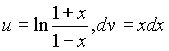 . Тогда
. Тогда 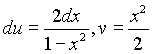 и F(x) =
и F(x) = 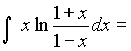 =
=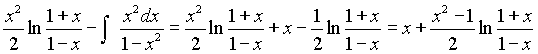 Несобственный интеграл будет равен
Несобственный интеграл будет равен ![]() = 1, так как
= 1, так как 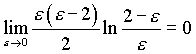
Искомая площадь вычисляется с помощью несобственного интеграла от неограниченной функции 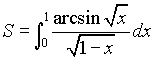 , который мы возьмем по частям, полагая
, который мы возьмем по частям, полагая 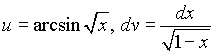 . Тогда
. Тогда 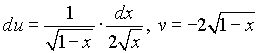 и
и