







|
|
|
|
|
||
Пример 1.
Вычислить объем тела, ограниченного параболоидом вращения z = x2 + y2 +1, координатными плоскостями и плоскостью x + y = 1.
рис. 3.13

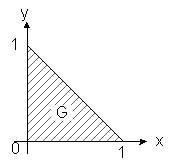
Данное тело представляет из себя цилиндр над треугольником, лежащим в плоскости XOY, с образующей, параллельной оси Z . Нижнее его основание - область G - прямоугольный треугольник с единичными катетами, сверху тело ограничено той частью поверхности z = x2 + y2 + 1, которая соответствует координатам ( x, y ) G(проектируется на область G). Вычислим данный объем при помощи двойного интеграла (см. п.3.5) по области G: ![]()
рис. 3.14
от функции f(x, y)=x2 + y2 + 1:

![]()
= 1 / 3 - 1 / 4 + 1 / 12 + 1 - 1 / 2 = 2 / 3.
Пример 2.
Вычислить объем тела, ограниченного параболоидами z = x2 + y2 ,
z = 2x2 +2y2 , цилиндром y = x2 и плоскостью y = x.
рис. 3.15

Данное тело является цилиндрическим. Его образующая параллельна оси Z,
направляющая боковой поверхности - замкнутая кривая, состоящая из части параболы y = x2 и отрезка прямой y = x при x [0,1] . Cверху и снизу тело ограничено параболоидами. Это тело представляет из себя область, элементарную относительно оси z и может быть описано следующим образом:
![]() = { ( x, y )
= { ( x, y )![]() G, x2 + y2
G, x2 + y2 ![]() z
z ![]() 2x2 + 2y2 },
2x2 + 2y2 },
где G ![]() R2 - область, правильная как относительно оси x, так и относительно оси y
R2 - область, правильная как относительно оси x, так и относительно оси y
G = { x![]() [0, 1], x2
[0, 1], x2 ![]() y
y ![]() x}.
x}.
Вычислим данный объем при помощи тройного интеграла (см. п.3.5) :


Пример 3.
Вычислить объем n - мерного симплекса Sn :
![]() .
.
Представим симплекс Sn как элементарную относительно оси xn область :
![]()
Используя теорему 2 пункта 3.4 , будем иметь


При n=1 интеграл равен длине отрезка [0, 1], при n=2 площади прямоугольного треугольника с катетами длины 1, при n=3 объему прямоугольной пирамиды с единичными перпендикулярными ребрами.