3.4. Уравнение Лапласа в прямоугольнике
Для решения уравнения Лапласа в прямоугольнике необходимо рассмотреть вспомогательную задачу.
  |
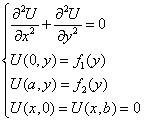(1) (2) (3) (4) |
Условие (4) необходимо. Оно нам поможет при решении.
Решим уравнение (1) методом разделения переменных
Уравнение (1) примет вид
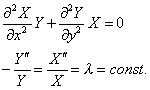
Отсюда получим два обыкновенных дифференциальных уравнения.
 . |
(5) (6) |
Необходимо определить знак 
.
1 случай.
Пусть 
Рассмотрим уравнение (5):
.
Характеристическое уравнение:
Рассмотрим уравнение (6)
.
Характеристическое уравнение:
Таким образом,
Удовлетворим краевым условиям (4):
так как мы ищем ненулевые решения уравнения (1), тогда C+D=0,
отсюда 
.
Учитывая, что
имеем:
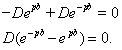
но тогда мы получим решение уравнения равное постоянной, а это не удовлетворяет
условиям (2), (3).
2 случай. Пусть
Рассмотрим уравнение (6)
.
Характеристическое уравнение:
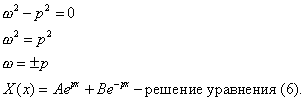
Рассмотрим уравнение (5):
.
Характеристическое уравнение:
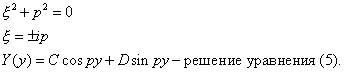
Удовлетворим начальному условию (4).
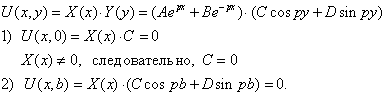
Помня, что С=0 имеем
Если D=0, то решение тождественно равно нулю, а нам это не подходит, значит
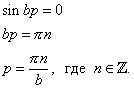
Запишем решение задачи в виде ряда:
 |
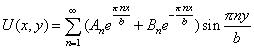(7) |
Удовлетворим начальным условиям (2), (3). Подставим в выражение (7) начальное условие (2):
.
 |
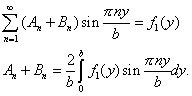(8) |
Удовлетворим начальному условию (3):
 |
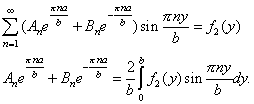(9) |
Для нахождения коэффициентов 
необходимо решить систему уравнений (8), (9):
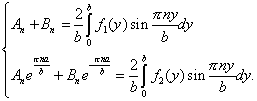
Подставив полученные коэффициенты в (7) получим решение задачи.
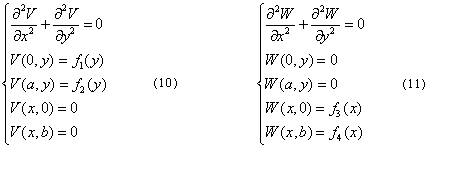
Рассмотрим ненулевые краевые условия для уравнения Лапласа в прямоугольнике:
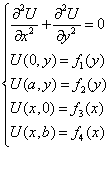
Ищем решение задачи в виде суммы двух функций
.
Задача (10) уже решена (см. вспомогательную
задачу), а чтобы найти решение задачи (11) необходимо просто заменить
соответствующие буквы и цифры в решении для V(x,t), то есть
