3.3. Задача Дирихле для уравнения Лапласа в кольце
Найти функцию U, удовлетворяющую уравнению
внутри кольца. |
(1) |
Необходимо поставить краевые условия на каждой из границ:
 |
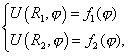(2) |
где 
-заданные
функции, 
-полярный
угол.
Для простоты вычислений возьмем
и 
тогда краевые условия примут вид
 |
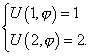(2*) |
Запишем уравнение (1) в полярных координатах
Решим уравнение методом разделения переменных, то есть будем искать решение уравнения (1) вида
.
Тогда уравнение (1) примет вид
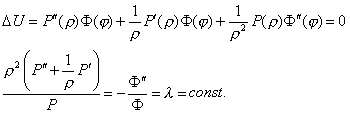
Отсюда получим два обыкновенных дифференциальных уравнения.
 |
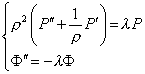(3) (4) |
Необходимо определить знак 
.
В уравнении Лапласа в круге мы выяснили, что 
и решения уравнений (3)-(4) имеет вид
и при 
получили
Общее решение имеет вид
Удовлетворим краевым условиям (2*). Необходимо выяснить, какие из коэффициентов являются лишними.
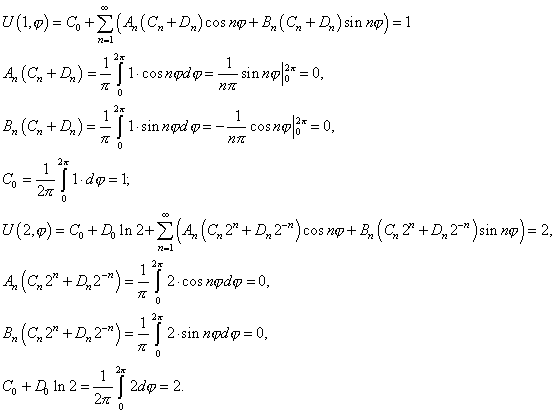
Итак, получили
 |