







|
|
|
|
|
||
Пример 1.
Вычислить тройной интеграл 
Данный тройной интеграл является повторным тройным интегралом, а потому его можно вычислять поэтапно, учитывая, что во внутреннем интеграле изменяется лишь переменная z , а x и y не изменяются (являются постоянными как функции от z ) и могут быть в силу этого вынесены из-под
знака интеграла при интегрировании по z. После проведения двойной подстановки приходим к двойному повторному интегралу , который вычисляем,
вынося из-под внутреннего интеграла x:


Пример 2.
Вычислить тройной интеграл  по области
по области ![]() , ограниченной гиперболическим параболоидом z = x y и плоскостями x + y =1 и z = 0 (z
, ограниченной гиперболическим параболоидом z = x y и плоскостями x + y =1 и z = 0 (z ![]() 0)
0)
Область ![]() является элементарной относительно оси z и может быть описана следующим образом:
является элементарной относительно оси z и может быть описана следующим образом:
![]()
где G ![]() R2- область плоскости ( x , y ), ограниченная прямой x + y = 1 и прямыми x = 0 и y = 0 - линиями пересечения гиперболического параболоида z = x y и плоскости z = 0 .
R2- область плоскости ( x , y ), ограниченная прямой x + y = 1 и прямыми x = 0 и y = 0 - линиями пересечения гиперболического параболоида z = x y и плоскости z = 0 .
рис 3.11
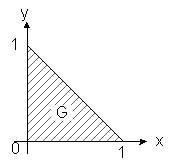
В свою очередь, G - треугольник на плоскости ( x , y ), является областью элементарной как относительно оси x (см. п.3.3) , так и относительно оси y (см. п.3.3) . Опишем G
G = {(x,y): 0 ![]() x
x ![]() 1, 0
1, 0 ![]() y
y ![]() 1 - x}.
1 - x}.
Используя эти представления областей ![]() и G и используя теорему 1 пункта 3.4 , перейдем от тройного интеграла к повторному тройному интегралу:
и G и используя теорему 1 пункта 3.4 , перейдем от тройного интеграла к повторному тройному интегралу:

Вычислим полученный повторный интеграл :

