Естественный способ задания движения точки

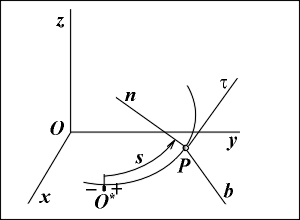
Рассмотрим, как вычисляются скорость и ускорение точки при естественном способе задания ее движения, то есть когда заданы траектория точки и закон движения точки вдоль этой траектории в виде s = s(t).

В этом случае векторы v и a определяют по их проекциям не на оси системы координат Oxyz, а на подвижные оси P nb, имеющие начало в точке Р и движущиеся вместе с нею (см.рис.). Эти оси, называемые осями естественного трехгранника, направлены следующим образом:

• ось P направлена по касательной к траектории в сторону положительного направления отсчета координаты s;
• ось Pn направлена по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории;
• ось Pb направлена перпендикулярно к первым двум осям P и Pn так, чтобы она образовала правую систему осей (с положительного направления оси Pb поворот оси P к оси Pn в их плоскости на прямой угол виден происходящим против хода часовой стрелки).

Определение скорости точки

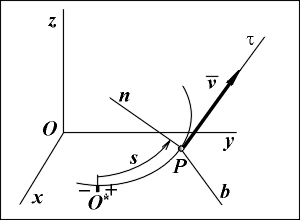
Вектор скорости v точки направлен по касательной к траектории и определяется одной проекцией , равной первой производной от криволинейной координаты s этой точки по времени:

= ds / dt = .

Модуль скорости v = | | и, следовательно, значения v и могут отличаться лишь знаком:

Таким образом, величина определяет одновременно и модуль скорости, и сторону, в которую направлен вектор v вдоль касательной.

Определение ускорения точки

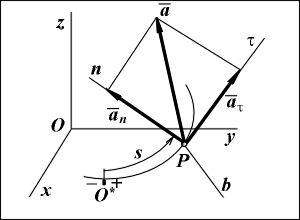
Вектор ускорения a точки лежит в соприкасающейся плоскости P n и определяется двумя проекциями и a_n (a_b = 0):

• проекция ускорения точки на касательную равна первой производной от алгебраической скорости или второй производной от криволинейной координаты точки по времени:

  = d / dt = d²s /dt² или = = .

• проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой:

  a_n = v² / .

Вектор ускорения a является векторной суммой касательной составляющей , напраленной вдоль касательной P , и нормальной составляющей a_n, направленной вдоль главной нормали Pn:

a = + a_n.

При этом составляющая может быть направлена или в положительном, или в отрицательном направлении оси P в зависимости от знака проекции , а составляющая a_n будет всегда направлена в сторону вогнутости кривой, так как проекция a_n 0.

Так как эти составляющие взаимно перпендикулярны, то модуль вектора a определяется по формуле:

a = ( ² + a_n² ) .

Рассмотрим теперь геометрическую характеристику траектории точки, называемую радиусом кривизны .

Радиус кривизны кривой в какой-либо ее точке равен радиусу окружности, которая наилучшим образом аппроксимирует по сравнению с другими окружностями участок кривой из малой окрестности рассматриваемой точки. Величина, обратная радиусу кривизны, называется кривизной кривой k = 1 / в данной точке.

В частности, для окружности радиус кривизны одинаков во всех ее точках и равен ее радиусу: = R (кривизна окружности k = 1 / R); для прямой радиус кривизны = (кривизна прямой k = 0).

Рассмотрим условия, при которых касательное и нормальное ускорения обращаются в нуль.

• Касательное ускорение равно нулю, если = d / dt = 0.
  Это условие выполняется, если все время v = | | = const, то есть при равномерном движении точки по траектории любой формы.
  Касательное ускорение обращается в нуль также в те моменты времени, в которые алгебраическая скорость достигает экстремума, например максимума или минимума.
• Нормальное ускорение равно нулю, если a_n = v² / = 0.
  Это условие выполняется, если = , то есть при прямолинейном движении точки. При движении точки по криволинейной траектории = в точках перегиба, в которых происходит изменение выпуклости траектории на вогнутость, и наоборот.
  Нормальное ускорение обращается в нуль также в моменты времени, в которые v = 0, то есть в моменты изменения направления движения точки по траектории.
  (Пример)

• касательное ускорение характеризует изменение вектора скорости по величине;
• нормальное ускорение характеризует изменение вектора скорости по направлению.