Предыдущий уровень изложения текущего раздела   Текущий уровень изложения предыдущего раздела   Текущий уровень изложения следующего раздела   Первый уровень изложения следующего раздела   Уровень:


Естественный способ задания движения точки

Пример. Точка движется по окружности радиуса R согласно закону (s - в метрах; t - в секундах):

s = 4t - t2, t 0.

Определить ускорение точки в момент ее остановки.

Решение.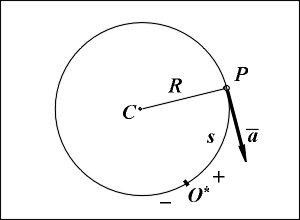

Вычислим алгебраическую скорость точки:

= = (4t - t2)· = 4 - 2t.

Остановка точки произойдет в момент времени t = t1 > 0, удовлетворяющий условию: (t1) = 0, откуда находим t1 = 2(c).

Вычисляем касательное ускорение точки в этот момент времени:

= = (4 - 2t)· = -2 (м/с2).

Поскольку в момент остановки точки v = 0, то нормальное ускорение an = v2 / R = 0. Тогда вектор ускорения a = , равен по модулю a = | | = 2 (м/с2) и направлен по касательной к окружности в сторону отрицательного направления отсчета координаты s.