







|
|
|
|
|
||
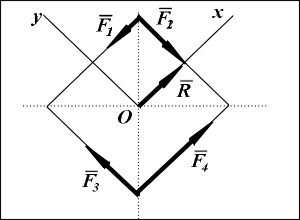
Пример. К вершинам квадрата со стороной a = 0.5(м) приложены силы: F1 = 4(Н); F2 = F3 = 8(Н); F4 = 12(Н). Определить главный вектор этой системы сил и ее алгебраический главный момент относительно центра квадрата О.
Решение. Введем координатную систему Oxy, оси которой параллельны сторонам квадрата ( в такой системе координат расчеты проводятся наиболее простым образом ).
Силы F2,F3 образуют пару сил с моментом M23 = -F2·a=-4(Н·м) и их можно не учитывать при вычислении проекций главного вектора R:
Rх = F1x + F4x = -F1 + F4= -4 + 12 = 8(Н);
Ry = F1y + F4y = 0.
Вычисление алгебраического главного момента LO проведем с использованием плеч сил F1 и F4, равных половине длины стороны квадрата (a/2):
LO = F1·a/2 - F4·a/2 + M23 = 1 - 4 + 3 = 0.
Таким образом, для заданной системы сил ее главный вектор равен по модулю R = 8(Н) и направлен вдоль оси Ox, а ее алгебраический главный момент LO = 0.
Замечание. В случае, когда LO = 0, главный вектор R является равнодействующей силой заданной системы сил.