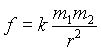Понятие напряженности магнитного поля построено на формальной аналогии полей неподвижных зарядов и неподвижных намагниченных тел. Такая аналогия часто оказывается весьма полезной, т.к. позволяет перенести в теорию магнитного поля методы, разработанные для электростатических полей.

Напряженность магнитного поля первоначально была введена в форме закона Кулона через понятие магнитной массы, аналогичной электрическому заряду, как механическая сила взаимодействия двух точечных магнитных масс в однородной среде, которая пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между ними

,

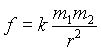где m1 и m2 - взаимодействующие магнитные массы; r - расстояние между точками, в которых магнитные массы считаются сосредоточенными; k - коэффициент, зависящий от свойств среды и системы единиц измерения.

Сила f направлена по прямой, соединяющей центры магнитных масс.

Магнитные массы одного знака отталкиваются, а противоположного - притягиваются.

Для количественной характеристики магнитного поля можно воспользоваться механической силой, действующей на положительный полюс пробного магнита, в той точке, где он расположен в пространстве. Напряженностью магнитного поля называется отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля.

Напряженность изображается вектором H, имеющим направление вектора механической силы f.

.

(1)

Если определить напряженность во всех точках магнитного поля, то можно построить линии, направление касательных к которым в каждой точке поля будет совпадать с направлением напряженности. Такие линии называются линиями напряженности или силовыми линиями.

Можно также ввести понятие о силовой трубке магнитного поля аналогично тому, как это было сделано для магнитного потока. Силовые линии, в отличие от линий индукции магнитного поля, начинаются на положительных магнитных массах и заканчиваются на отрицательных, т.е. прерываются.

Для изотропной среды существует связь между индукцией и напряженностью магнитного поля

или .

(1)

Последнее соотношение можно использовать для определения магнитной проницаемости m как отношения индукции к напряженности магнитного поля.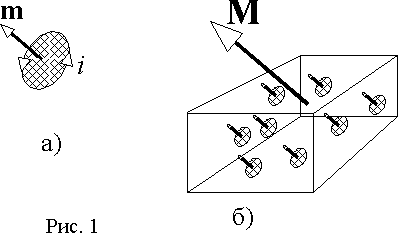

При помещении в магнитное поле вещества в нем происходят процессы ориентации различных структур, обладающих дипольным магнитным моментом.  Так электроны, перемещаясь по орбитам, образуют элементарные токи и соответствующие магнитные поля или магнитные диполи (рис. 1 а)). Кроме этого, электроны создают магнитный момент за счет вращения вокруг собственной оси, называемый спиновым магнитным моментом.

Магнитный диполь можно характеризовать вектором магнитного момента, численно равным произведению величины элементарного тока на площадь контура, ограниченного этим током в пространстве

m = is,

и направленным по нормали к площади контура.

Геометрическая сумма всех магнитных моментов образует магнитный момент тела

M = S m,

который обычно соотносят с объемом вещества V и называют намагниченностью или интенсивностью намагничивания

.

(1)

Единицу измерения намагниченности можно определить из выражения (1) [J] = [M/V] = Ам2/м3 = А/м.

Вектор намагниченности совпадает с направлением вектора напряженности и связан с ним линейной зависимостью

.

(2)

Безразмерный коэффициент k называется магнитной восприимчивостью вещества.

Для магнитного поля, существующего в некоторой среде, можно представить магнитную индукцию в виде суммы двух составляющих, индукции B0 , соответствующей вакууму, и дополнительной индукции Bн, создаваемой намагниченностью вещества

,

(3)

где m 0 - магнитная проницаемость вакуума; m а и m =1+k - соответственно абсолютная и относительная магнитные проницаемости вещества.

В зависимости от значения m все вещества разделяются на диамагнитные парамагнитные и ферромагнитные. К диамагнетикам относятся вещества, у которых k <0 и m <1, т.е. их магнитная проницаемость меньше чем у вакуума. Наиболее сильно диамагнитные свойства выражены у висмута, у которого m =0,99983. У парамагнетиков k >0 и m >1. Например, у платины относительная магнитная проницаемость составляет 1,00036.

Особую группу веществ, представляющих большой интерес с практической точки зрения, составляют ферромагнетики, у которых m >>1 и составляет величину порядка 104ј 106.

Определение напряженности магнитного поля через магнитные силы и массы не вполне адекватно физической картине явлений в магнитном поле, т.к., в отличие от электрического заряда, не существует массы или заряда магнитного. На практике удобнее пользоваться явлениями, связывающими между собой электрический ток и магнитное поле.

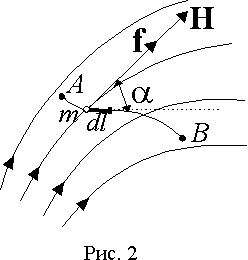
Пусть некая точечная магнитная масса m перемещается по произвольному пути из точки A в точку B магнитного поля (рис. 2). Действующая на магнитную массу механическая сила f в любой точке поля направлена по касательной к силовой линии и равна f=mH , где H - напряженность поля.

Работа по перемещению массы m по пути AB равна

,

(4)

где a - угол между направлением вектора H и касательной к направлению перемещения. В этом выражении линейный интеграл вектора напряженности магнитного поля, взятый вдоль некоторого пути AB, называется магнитодвижущей силой (МДС) F, действующей вдоль этого пути

,

(5)

т.е. магнитодвижущая сила численно равна работе по перемещению единичной магнитной массы по заданному пути.

Рассмотрим теперь перемещение магнитной массы m по замкнутому пути в магнитном поле витка с постоянным значением тока i.

Сначала допустим, что существует только воздействие со стороны поля витка на массу m (рис. 3 а)).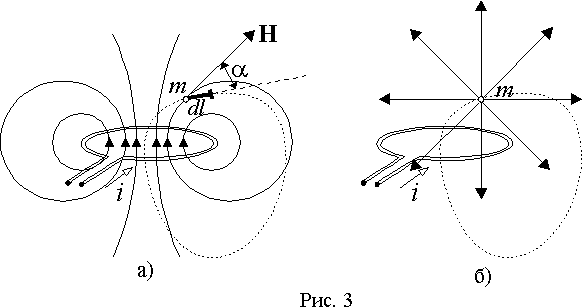

В соответствии с выражением (4), работа перемещения по замкнутому пути будет равна

.

(6)

Теперь предположим, что мы перемещаемся по тому же замкнутому контуру, но воздействие существует только со стороны магнитной массы m на виток с током (рис. 3 б)). При анализе электромагнитной силы было установлено, что элементарная работа по перемещению отрезка проводника с током i в магнитном поле равна dA = idФ = idN, где - число линий индукции магнитного поля, пересекаемых при перемещении.

Если магнитная масса m переместится по изображенному на рисунке контуру, то виток пересечет все исходящие из нее линии индукции и работа по перемещению, с учетом того, что полный магнитный поток перемещаемой массы численно равен ее значению, будет равна

.

(7)

Но на основании закона сохранения энергии A1 = A2 , отсюда

.

(8)

Очевидно, что задачу можно дополнить другими контурами (витками) с токами. Однако, в этом случае ее можно рассмотреть по отдельности, для каждого витка. Тогда в правой части выражения (8) окажется алгебраическая сумма всех токов, охваченных контуром интегрирования

.

(9)

Полученное выражение называется законом полного тока. Линейный интеграл вектора напряженности магнитного поля, взятый по замкнутому контуру, равен полному (суммарному) электрическому току, проходящему через поверхность, ограниченную этим контуром или МДС вдоль замкнутого контура равна полному току, охватываемому этим током.

Закон полного тока является одним из важнейших законов, устанавливающим неразрывную связь между электрическим током и магнитным полем. Из него следует, что любая магнитная линия обязательно охватывает электрический ток и, наоборот, электрический ток всегда окружен магнитным полем. Причем, не являются исключением из этого закона и постоянные магниты, т.к. в них магнитные линии создаются элементарными микроскопическими токами, также входящими в правую часть выражения (9).

Переход магнитного потока из одной среды в другую сопровождается некоторыми явлениями на границе раздела этих сред.

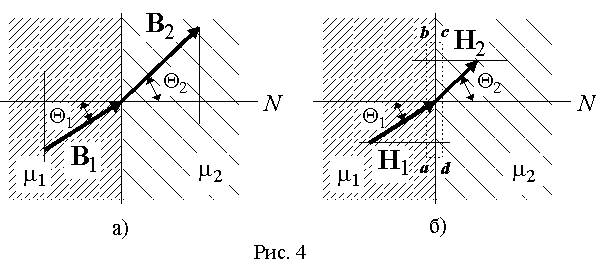
Пусть магнитный поток переходит из среды с магнитной проницаемостью m 1 в среду с магнитной проницаемостью m 2 (рис. 4). Из условия непрерывности магнитного потока следует, что при переходе из одной среды в другую через границу раздела площадью S он должен сохраняться, т.е. Ф1 = Ф2 . Но магнитный поток для изотропной среды можно представить через индукцию в виде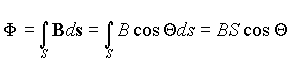

,

где Q - угол между направлением вектора индукции и нормалью к поверхности границы раздела сред, а произведение BcosQ - проекция вектора индукции на нормаль или нормальная проекция.

Отсюда - Ф1= B1ScosQ 1= Ф2= B2ScosQ 2 или

B1cosQ 1 = B2cosQ 2 ,

(10)

т.е. при переходе из одной среды в другую магнитная индукция изменяет свое значение, но сохраняет нормальную проекцию.

В изотропной среде векторы индукции и напряженности магнитного поля совпадают по направлению, поэтому и углы с нормалью векторов H1 и H2 будут такими же как у векторов B1 и B2 (рис. 4 б)). Выделим вблизи поверхности раздела замкнутый прямоугольный контур abcd так, чтобы его противоположные стороны длиной l располагались в разных средах на бесконечно малом расстоянии от границы (рис. 4 б)).Найдем линейный интеграл от вектора напряженности поля вдоль этого контура и по закону полного тока приравняем его нулю, т.к. внутри контура отсутствует электрический ток: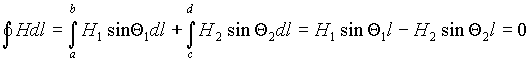

.

Отсюда -

H1sinQ 1 = H2sinQ 2 .

(11)

Это означает, что при переходе из одной среды в другую вектор напряженности магнитного поля сохраняет тангенциальную составляющую, т.е. проекцию на границу раздела сред.

Если разделить выражение (10) на выражение (11), то мы получим соотношение, связывающее углы векторов с нормалью и магнитные проницаемости -

.

(12)

Из выражения (12) следует, что при большом отличии магнитных проницаемостей (m 1/m 2=1000), например, при выходе магнитного потока из ферромагнетика в воздушную среду почти параллельно границе раздела (Q 1=87° ), угол с нормалью вектора индукции составит около 1° , т.е. можно считать, что магнитные линии в воздухе нормальны к поверхностям тел из ферромагнетиков.

ЗАДАЧА