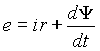Рассмотрим механические проявления магнитного поля. Из опыта известно, что проводники с током расположенные в магнитном поле испытывают механическое воздействие. Силы, действующие на проводники или тела из ферромагнитного материала, называются электромагнитными или электродинамическими силами.

Если по какому-либо проводнику протекает электрический ток i, то ЭДС внешнего источника e уравновешивается падением напряжения на его резистивном сопротивлении r и ЭДС, создаваемой пококосцеплением Y

.

(1)

Отсюда работа, совершаемая внешним источником ЭДС за время dt

.

(2)

Первое слагаемое соответствует потерям энергии на нагревание проводника, а второе работу внешнего источника dA, связанную с процессами в магнитном поле

.

(3)

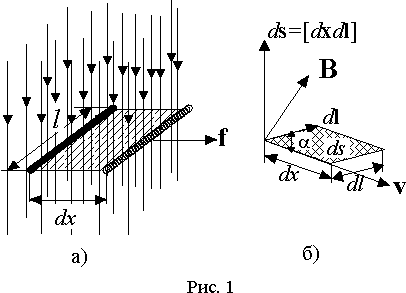
Пусть в однородном магнитном поле находится линейный проводник длиной l, по которому протекает ток i (рис.1 а)). Со стороны поля на него действует электромагнитная сила f, вследствие чего, он смещается на расстояние dx. Согласно выражению (3)

.

(4)

Отсюда

(5)

В общем случае, когда проводник имеет произвольную форму и расположение в магнитном поле в выражении (5) нужно перейти к бесконечно малым приращениям. При перемещении элементарного отрезка длиной dl на расстояние dx (рис. 1 б)) приращение магнитного потока получается равным

dФ=Bcosb ds=Bcosb dldx,

где b - угол между направлением вектора B и нормалью к поверхности ds=dlЧ dx, описываемой элементарным отрезком dl в пространстве. Подставляя это выражение в (5) получим

или в векторной форме

(6)

.

(7)

ЗАДАЧА 1

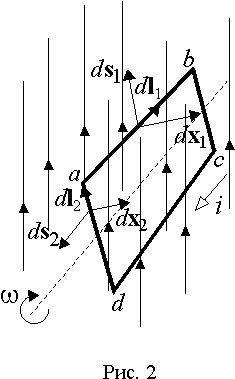
Рассмотрим важный с практической точки зрения случай воздействия электромагнитных сил на прямоугольную рамку с током, находящуюся в однородном магнитном поле, подвешенную на оси вращения перпендикулярной линиям индукции (рис. 2).

На каждый элементарный отрезок сторон ab и ad в соответствии с выражением (6) будут действовать электромагнитные силы df1=iBcosb 1dl1 и df2=iBcosb 2dl2, но b 2 = 90° , поэтому на участки bc и ad со стороны магнитного поля никакого воздействия оказываться не будет.

При вращении рамки угол b 1 будет функцией времени b 1= w t . Отсюда сила, действующая на сторону ab рамки

,

(8)

где ab - длина стороны ab. Тогда вращающий момент, создаваемый электромагнитной силой или электромагнитный вращающий момент, действующий на рамку со стороны магнитного поля

,

(9)

где s - площадь рамки.

Это выражение можно получить также непосредственно из выражения (3), если работу по вращению рамки представить через электромагнитный вращающий момент и элементарный угол ее поворота da

dA = Mda = idY ,

(10)

но для вращающейся рамки a = w t, а da = d(w t) = w dt. Отсюда

.

(11)

Если угол между направлением вектора индукции и плоскостью рамки по-прежнему обозначить b , то потокосцепление рамки будет синусной функцией этого угла, т.е. Y = Y m sin b . Подставляя значение Y в выражение (11) с учетом того, что Y m=Bs , получим

.

(12)

Как и следовало ожидать, выражения (9) и (12) тождественны. Они были получены для рамки состоящей из одного витка, но в случае рамки с числом витков w потокосцепление Y возрастет на число витков, поэтому для такой рамки электромагнитный момент

.

(13)

В неподвижной рамке также будет действовать электромагнитный момент, величина которого легко находится, если учесть, что выражения (9) и (12) были получены представлением угла b между плоскостью рамки и направлением вектора индукции магнитного поля непрерывной функцией времени b = w t. Следовательно,

.

(14)

Таким образом, электромагнитный вращающий момент, действующий на рамку с током, является синусоидальной функцией угла ее поворота, и его амплитуда пропорциональна току в рамке, величине индукции магнитного поля, площади рамки и числу витков в ней.

ЗАДАЧА 2