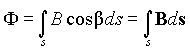
(4)
В пространстве, окружающем проводники, по которым протекает электрический ток, а также окружающем постоянные магниты, существует ряд физических явлений, проявляющихся в возникновении ЭДС в движущихся проводниках, механическом воздействии на постоянные магниты и проводники с током, находящиеся в этом пространстве и др.
Пространство, в котором происходят эти явления, называется магнитным полем
.Для определения количественных характеристик магнитного поля можно использовать любое его проявление, однако обычно используют явление электромагнитной индукции и механическое воздействие со стороны поля.
Явление электромагнитной индукции заключается в возникновении
ЭДС проводниках. Причем, условия, при которых она возникает могут быть самыми различными. Это может происходить, например, при движении проводника в однородном магнитном поле или в неподвижном проводнике, находящемся в переменном магнитном поле.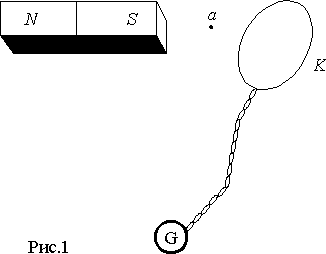
Определить основные соотношения для этого явлении можно с помощью устройства показанного на рис. 1. Оно представляет собой тонкий проводник, изогнутый в виде кольца
K и подключенный гибким витым проводом к баллистическому гальванометру G. Отклонение стрелки баллистического гальванометра пропорционально количеству зарядов q, протекших через него.Если центр кольца
K помещать в разные точки пространства вокруг постоянного магнита, а затем быстро относить на значительное расстояние, то гальванометр будет фиксировать разные значения q. Расстояние, на которое нужно удалять кольцо теоретически должно быть бесконечным для того, чтобы все проявления поля были сведены к нулю.При повторении опыта из одной и той же точки пространства мы будем получать одинаковые значения
q, но если изменить сопротивление цепи r, по которой протекают заряды, то величина q изменится обратно пропорционально r. Отсюда можно сделать заключение, что каждая точка пространства вокруг постоянного магнита обладает некоторым свойством, определяющим количество зарядов q, протекающих через гальванометр при удалении кольца K на значительное расстояние от магнита. Обозначим это свойство символом Ф и назовем его магнитным потоком, оставляя пока смысловое обоснование термина. Тогда можно записать отмеченную выше связь в виде выражения:|
(1) |
Повторим опыты с кольцом в одной и той же точке пространства постоянного магнита, например, в точке
a рис. 1, при неизменном сопротивлении цепи и положении плоскости кольца. При этом будем постепенно изменять площадь кольца. Если площадь кольца достаточно малая, то изменения количества зарядов D q будут в точности пропорциональны изменению площади кольца D s. Но количество зарядов пропорционально величине магнитного потока, поэтому и изменения магнитного потока пропорциональны изменению площади, т.е.|
D Ф = BaDs или, переходя к бесконечно малым, dФ = Bads , |
(2) |
где величина
Ba не зависит от размеров кольца и определяется только положением точки a, следовательно, она характеризует магнитное поле в данной точке пространства и называется магнитной индукцией.Если опыты в точке
a продолжить, изменяя положение плоскости кольца в начальный момент, то можно установить, что существует такое его положение, при котором количество зарядов будет максимальным и всякое отклонение от этого положения будет приводить к их уменьшению пропорционально косинусу угла отклонения. Включая это условие в выражение (2) получим|
(3) |
где
b - угол между направлением нормали к плоскости пробного витка и направлением, при котором количество зарядов, протекающих через виток максимально.Выражение (3) показывает, что магнитная индукция B является векторной величиной и ее направление совпадает с направлением нормали к плоскости пробного витка, при котором количество зарядов, протекающих через виток при его удалении на значительное расстояние, максимально.
Опыты с пробным витком (кольцом) можно проводить также и в пространстве катушки, подключенной к источнику постоянного тока. При этом вместо удаления витка можно просто выключать ток, т.к. в обоих случаях магнитный поток будет уменьшаться до нуля.
Если в пространстве выделить некоторую поверхность
s, то магнитный поток через эту поверхность определится из выражения (3) в виде|
|
(4) |
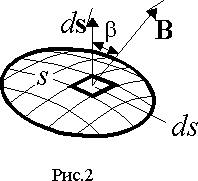
где
ds - вектор численно равный поверхности ds и имеющий направление нормали к этой поверхности (рис 2.).Из выражения (4) следует, что
магнитный поток является потоком вектора магнитной индукции через некоторую поверхность. Единицей магнитного потока является вебер (1 Вб = 1 ВЧс).Если поверхность
ds нормальна к вектору B, то cosb = 1 и из выражения (3)|
|
(5) |
т.е.
магнитная индукция является плотностью магнитного потока в данной точке поля. Единицей магнитной индукции является тесла (1 Тл = 1 Вб/м2).Возвращаясь к полученному ранее
выражению (1), можно количественно определить магнитный поток через некоторую поверхность как произведение величины заряда, протекающего через проводник совмещенный с границей этой поверхности при полном исчезновении магнитного поля, на сопротивление электрической цепи, по которой протекают эти заряды.В описанных выше опытах с пробным витком (кольцом), он удалялся на такое расстояние, при котором исчезали всякие проявления магнитного поля. Но можно просто перемещать этот виток в пределах поля и при этом в нем также будут перемещаться электрические заряды. Перейдем в выражении (1) к приращениям
|
Ф + D Ф = r(q - D q) Ю D Ф = - rD q Ы D q = - D Ф/r |
(6) |
где
D Ф и D q - приращения потока и количества зарядов. Разные знаки приращений объясняются тем, что положительный заряд в опытах с удалением витка соответствовал исчезновению поля, т.е. отрицательному приращению магнитного потока.С помощью пробного витка можно исследовать все пространство вокруг магнита или катушки с током и построить линии, направление касательных к которым в каждой точке будет соответствовать направлению вектора магнитной индукции
B (рис. 3)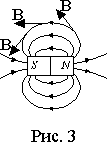
Эти линии называются линиями вектора магнитной индукции или магнитными линиями
. B, а количество линий, проходящих через любую поверхность равно значению магнитного потока.Магнитные линии непрерывны
и этот принцип можно математически представить в виде|
|
(7) |
т.е. магнитный поток, проходящий через любую замкнутую поверхность равен нулю
.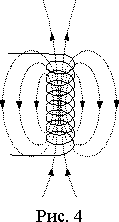
Выражение (4) справедливо для поверхности s любой формы. Если рассматривать магнитный поток проходящий через поверхность, образованную витками цилиндрической катушки (рис. 4), то ее можно разделить на поверхности, образованные отдельными витками, т.е. s=s1+s2+...+s8. Причем через поверхности разных витков в общем случае будут проходить разные магнитные потоки. Так на рис. 4, через поверхности центральных витков катушки проходят восемь единичных магнитных линий, а через поверхности крайних витков только четыре.
Для того, чтобы определить полный магнитный поток, проходящий через поверхность всех витков, нужно сложить потоки, проходящие через поверхности отдельных витков, или, иначе говоря, сцепляющиеся с отдельными витками. Например, магнитные потоки, сцепляющиеся с четырьмя верхними витками катушки рис. 4, будут равны: Ф1=4; Ф2=4; Ф3=6; Ф4=8.
Общий магнитный поток
, сцепляющийся со всеми витками катушки, называется потокосцеплением и численно равен сумме потоков, сцепляющихся с отдельными витками, т.е.|
Y = 2(Ф1+ Ф2+ Ф3+ Ф4) = 48 |
(8) |
Часто реальное распределение потокосцепления по виткам катушки неизвестно, но его можно принять равномерным и одинаковым для всех витков, если реальную катушку заменить эквивалентной с другим числом витков
wэ, сохраняя при этом величину потокосцепления Y = wэФm, где Фm - поток, сцепляющийся с внутренними витками катушки, а wэ - эквивалентное или эффективное число витков катушки. Для рассмотренного на рис. 4 случая wэ=Y /Ф4=48/8=6.Можно также произвести замену реальной катушки на эквивалентную с сохранением числа витков
Y = wФn. Тогда для сохранения потокосцепления необходимо принять, что со всеми витками катушки сцепляется магнитный поток Фn= Y /w .Первый вариант замены катушки эквивалентной сохраняет картину магнитного поля, изменяя параметры катушки, второй - сохраняет параметры катушки, изменяя картину магнитного поля.