Опр.1
Опр.2
8. Обобщенные функции
8.1. Понятие обобщенной функции
Понятие обобщенной функции позволяет выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, плотность точечного заряда.
Попытаемся определить плотность, создаваемую
материальной точкой массы, равной единице. Чтобы определить эту плотность,
распределим (или, как говорят, “размажем”) единичную массу равномерно
внутри окрестности радиуса 
с центром в нуле. В результате получим среднюю плотность 
,
равную
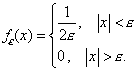
Но нас интересует плотность при 
.
Обозначим ее через 
.
Причем сначала в качестве искомой плотности возьмем поточечный предел
последовательности средних плотностей
при 
,
то есть функцию
и интеграл от этой функции по всей оси давал бы полную массу вещества, то есть
.
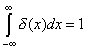Но с математической точки зрения, такое
невозможно, так как для функции 
,
определенной нашим способом:
.
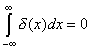Это значит, что данная функция не восстанавливает массу и поэтому не может быть принята в качестве искомой плотности. Итак, поточечный предел последовательности средних плотностей не подходит для наших целей. Поэтому требуются корректные определения для этого случая.
Выход состоит в том, чтобы искать другой,
так называемый, слабый предел последовательности .
А именно, будем рассматривать не предел
в каждой точке x, а предел следующих интегралов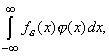 
где 
-произвольная
непрерывная функция. Ясно, что
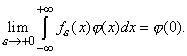
Эта формула обозначает, что слабым пределом
последовательности функций 
при
является оператор, точнее функционал, сопоставляющий каждой непрерывной
функции
число 
-ее
значение в точке 
.
Вот этот функционал мы и примем в качестве искомой плотности ,
это и есть известная 
Дирака.
Можно ли представить 
-функцию
в виде: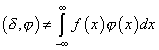 
с какой-либо локально интегрируемой функцией?
Для этого нужно, чтобы 
при 
.
Но такой функции нет.
Определение. Задать вещественный
функционал f на множестве функций M значит указать правило,
по которому каждой функции 
сопоставляется
вещественное число. Мы будем рассматривать в качестве множества M
совокупность
вещественных функций ,
которые определены при 
,
непрерывны и имеют производные любого порядка. Кроме того, будем предполагать,
что функции финитны,
то есть в случае конечного интервала (a,b) существуют такие окрестности
точек a и b (свои для каждой из функций ),
где эти функции обращаются в нуль. В случае бесконечного интервала (a,b),
кроме того, существует такая постоянная A, причем для каждой из функций
-своя,
что вне интервала (-A,A) функция обращается
в нуль. Такие функции
будем называть основными, а всю их совокупность D(a,b)-основным
пространством.
Пример, такой функции представлен на рисунке 2.
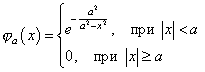
Проверим, что данная функция является основной.
Для этого достаточно показать, что она бесконечно-дифференцируема. Во
всех точках кроме 
это свойство очевидно. Проверим его выполнение в точке
.
.
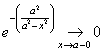
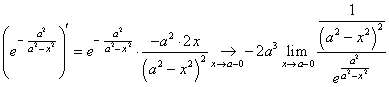Пусть 
,
тогда по правилу Лопиталя
,
то есть функция дифференцируема.
Аналогично проверяется непрерывность производной
любого порядка. В этом легко убедиться, заметив, что 
для любого непрерывного n.
Чтобы определить пространство основных функций D(a,b), нужно задать действия с ними. Точнее, надо проверить, что линейные операции не выводят из множества основных функций.
1. 
,
причем сумма конечна, то есть 
.
Если 
-основная
функция, то 
-основная
функция.
2. 
,
где 
- конечное число.
Если 
-
основная функция, то -основная
функция.
Линейный оператор, который каждому элементу пространства ставит в соответствие число, называется линейным функционалом (вещественным или комплексным).
.
Будем обозначать действие функционала f
на основную функцию
следующим образом:
.
Обобщенная функция (распределение)–это линейный непрерывный функционал на пространстве основных функций, то есть функционал f , удовлетворяющий условиям:
1.
,
где 
(линейность);
2.
Если 
в D,
то 
(непрерывность).
Если 
-локально
интегрируемая функция, то есть интегрируемая на любом конечном отрезке,
то можно рассматривать следующий линейный непрерывный функционал:
 . |
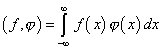(1) |
Проверим свойства 1-2.
1.
2.
,
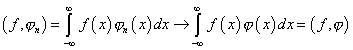то есть функционал непрерывен.
Функционал, представимый в форме (1), будем
называть регулярной обобщенной функцией, при этом будем говорить,
что данная обобщенная функция порождается локально-интегрируемой функцией
f, если его нельзя так представить, то–сингулярной. В частности,
рассмотренная выше
является сингулярной 
Другой пример сингулярной обобщенной функции.
Обобщенная функция 
.
Функция
не является локально-интегрируемой (она не является интегрируемой в окрестности
нуля). Тем не менее для любой основной функции можно образовать выражение
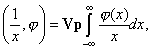
где интеграл понимается как главное значение в смысле Коши, то есть как
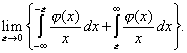
Можно получить и другое представление
для функцилнала, которое иногда бывает более удобным.
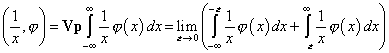
Сделаем замену, пусть 
,
тогда
.
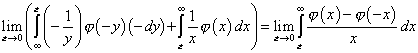