Опр. 1
Опр. 2
8.2. Действия с обобщенными функциями
Линейная комбинация обобщенных
функций определяется как линейная комбинация функционалов
Произведение любых двух обобщенных функций
определить сколько-нибудь естественным образом, по-видимому, невозможно,
но вполне естественно определяется произведение любой обобщенной функции
f на бесконечно дифференцируемую функцию 
.
Если f порождена локально-интегрируемой функцией, то для любой
основной функции 
.
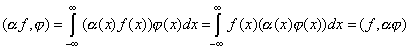Произведением 
произвольной
обобщенной функции f на бесконечно дифференцируемую функцию
называется обобщенная функция g, действующая по формуле
.
Очевидно, что функционал g линеен и непрерывен.
Определим производную обобщенной функции.
Для обычных функций операция дифференцирования не всегда выполнима. Существуют
функции, не имеющие производных в обычном смысле слова. Естественное определение
производных от обобщенных функций оказывается таким, что оно применимо
к любой обобщенной функции, то есть обобщенные функции имеют производные
всех порядков.
Чтобы дать это определение, рассмотрим сначала непрерывно дифференцируемую
функцию f(x). Она и ее производная будут локально-интегрируемыми,
поэтому порождают обобщенные функции, причем
Проинтегрируем по частям и воспользуемся
финитностью функции 
,
вследствие которой внеинтегральный член обратится в нуль. Следовательно,
.
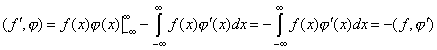Это равенство и положим в основу общего определения производной обобщенной
функции.
Пусть f–произвольная обобщенная функция.
Тогда функционал g, заданный формулой 
называем производной от f и обозначаем через 
или 
.
Этот функционал линеен
и непрерывен.
Свойства производной:
1. 
2.-
бесконечно дифференцируема, f – обобщенная
функция, тогда
