Опр. 1
Опр. 2
7.2.2. Уравнение Вольтерра с разностным ядром
Рассмотрим случай, когда ядро
K(s,t) зависит от разности
аргументов:
,
то есть уравнение имеет вид
  . |
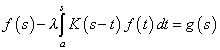(1) |
Метод решения уравнений данного типа состоит в использовании преобразования Лапласа.
Функция F называется
преобразованием Лапласа (изображением) функции f
(оригинала), если
.
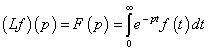Сверткой 
функций 
и 
называется
функция, определяемая следующим образом:
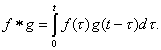
Применим преобразование Лапласа
к решению уравнения Вольтерра (1). Если g(s) и K(s)
достаточно гладкие функции, растущие при 
не быстрее показательной функции, так что
то применяя метод последовательных приближений, можно показать, что в этом случае f(s) будет удовлетворять экспоненциальной оценке
.
Следовательно, может быть найдено изображение по Лапласу функций f(s), K(s), g(s). Применяя к обеим частям уравнения (1) преобразование Лапласа и используя свойство преобразования Лапласа, находим
,
отсюда 
.
Оригинал f(s) для F(p) будет решением интегрального уравнения (1).
Основные свойства
преобразования Лапласа 
:
1.
линейно,
2. 
,
3. 
.
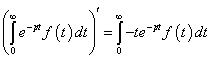
4.
Частный случай:
5.
где
.
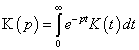
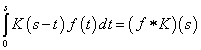Таблица изображений некоторых элементарных функций:
|
f (оригинал) |
F (изображение) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Существует два пути вычисления обратного преобразования Лапласа:
1. По общей формуле;
2. Для случая, когда изображение является рациональной функцией.
1). Рассмотрим первый
случай.
.
Пусть все полюса 
на комплексной плоскости расположены левее некоторой прямой, параллельной
мнимой оси.
Формула обращения имеет вид:
,
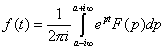где интеграл пробегает по всей
указанной прямой.
Решение 
находится по сумме вычетов:
,
где 
- особые точки 
.
2). Теперь рассмотрим второй способ, а именно, метод разложения рациональной дроби на простейшие.
Рассмотрим его на конкретном примере:
Приравняем числитель исходного выражения после приведения к общему знаменателю дробей с неопределенными коэффициентами:
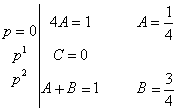
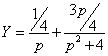
Применим обратное преобразование
Лапласа, получим ответ
.