7.2. Уравнение Вольтерра
7.2.1. Уравнение Вольтерра второго рода
Объяснение начнем с рассмотрения уравнения Фредгольма второго рода
  |
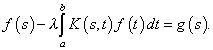(1) |
Ядро интегрального уравнения зададим следующим образом:
 , |
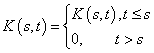(2) |
то есть ядро интегрального уравнения обращается
в нуль при условии, что вторая переменная больше первой, 
при
.
Подставив ядро (2) в уравнение
(1), получим частный случай уравнения Фредгольма
-
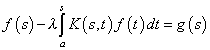уравнение Вольтерра.
Считаем, что 
-
непрерывная функция при 
,
и 
-
непрерывная функция в треугольнике 
и
при .
Таким образом, на диагонали 
ядро
имеет разрыв первого рода, если 
.
Все основные теоремы и аппарат,
изложенный для уравнения Фредгольма, сохраняются.
Ищем, как и раньше, решение
в виде ряда
 . |
(3) |
Для функции 
получаем формулы
.
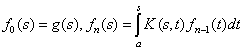
На промежутке или на квадрате имеем оценки для непрерывных функций:
и, проводя оценки для 
,
получаем последовательно:
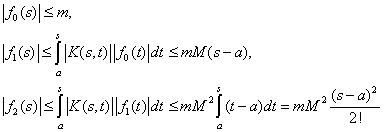
и вообще,
 |
(4) |
Докажем методом математической
индукции.
База индукции: при n=1
неравенмтво (4) верное.
Пусть неравенство (4) для -
верно, найдем оценку для 
.
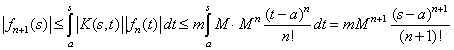Доказано.
При изменении s на конечном промежутке [a,b] члены ряда (3) по модулю не превышают чисел
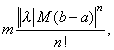
образующих при любом 
сходящийся ряд, и, следовательно, ряд (3)
сходится абсолютно и равномерно на [a,b], а его сумма есть непрерывная
функция, удовлетворяющая исходному уравнению. Аналогично можно построить
резольвенту
где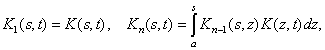 
причем из этих формул следует,
что 
при t>s.
Как и выше, доказывается абсолютная
и равномерная сходимость ряда для резольвенты при всех .
Таким образом, для уравнения Вольтерра резольвента
есть целая, то есть аналитическая на всей плоскости, функция, и при всяком
это уравнение имеет единственное решение, которое определяется формулой:
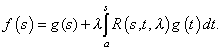
Можно утверждать, что уравнение Вольтерра не имеет характеристических значений, то есть однородное уравнение
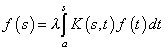
при любом
имеет только нулевое решение. В связи с этим, если бы мы построили для
уравнения (1) знаменатель Фредгольма
,
то оказалось бы, что он вовсе не имеет корней.
Докажем, что
напрямую.
Доказательство:
.
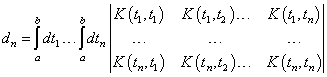Пусть 
,
для любого i при 
.
.
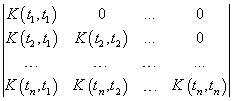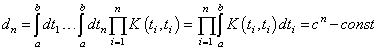
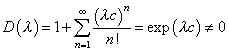Доказано.