7.1.3. Ряд Фредгольма
Объясним процедуру построения решения, предложенную Фредгольмом, но не будем проводить доказательство. Фредгольм заметил, что интегральное уравнение
имеет сходство с алгебраической системой.
Действительно, если мы разобьем промежуток
[a,b]
на n равных частей, длина каждой
из которых будет 
,
то интеграл можно заменить на интегральную сумму: 
,
где 
.
.
Распишем это уравнение в разных точках 
.Причем
на каждом интервале за
берется крайняя правая точка, 
,
то есть получаем систему уравнений
с n неизвестными.
,
где 
-неизвестны.
Решение осуществляется по формуле Крамера,
после чего, измельчая разбиение отрезка и переходя к пределу
при 
,
получим решение уравнения. Не приводя
эти выкладки, укажем лишь результат. Решение находится с помощью резольвенты
.
-
знаменатель Фредгольма,
где 
определяются с помощью рядов:
,
где
,
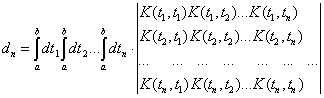
где
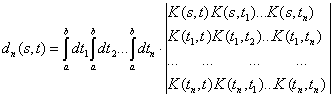
Ряды Фредголма имеют серьезное преимущество
перед рядами Неймона. Если ряд Неймана сходится в некотором круге, то
ряды 
и 
сходятся на всей комплексной плоскости за исключением корней уравнения
.