Опр. 1
Опр. 2
Опр. 3
7. Интегральные уравнения
7.1.
Уравнения Фредгольма
7.1.1.
Уравнение Фредгольма второго рода
Интегральное уравнение – это уравнение, в котором неизвестная функция находится под знаком интеграла. Например, уравнение
где 
-
известные функции, f необходимо найти,
-
постоянный параметр,
называется ядром интегрального уравнения.
Переменные s и t пробегают
здесь некоторый фиксированный отрезок 
.
Будем рассматривать линейные интегральные уравнения двух типов:
- уравнение
Фредгольма,
- уравнение
Вольтерра (частный случай уравнения
Фредгольма).
-
интегральное уравнение Фредгольма второго
рода.
- ядро интегрального оператора,
- заданный параметр,
- заданная функция;
-
искомая функция.
Если 
,
то уравнение однородное, если же 
,
то уравнение неоднородное.
Интегральное уравнение вида
называется интегральным уравнением Фредгольма первого рода.
Если интеграл имеет переменный верхний или нижний предел, то интегральное уравнение Фредгольма переходит в новый класс уравнений - интегральное уравнение Вольтерра.
- интегральное уравнение Вольтерра второго рода,
- интегральное уравнение Вольтерра первого рода.
Рассмотрим решение интегрального уравнения Фредгольма второго рода
| . |
(1) |
мы считаем комплексной непрерывной функцией двух переменных 
в
квадрате 
Введем обозначение
и запишем уравнение (1) в операторном виде , |
(2) |
где M- интегральный оператор с ядром
.
Величина нормы М (то
есть 
)
зависит от пространства, в котором
ведется рассмотрение.
Для разрешимости уравнения (2) достаточно
выполнения условия 
.
Это условие, например, в пространстве 
сведется
к следующему:
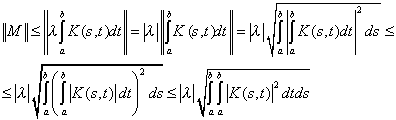
Итак, если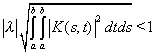 
,
то по теореме, рассмотренной в разделе
6.5.4. главы 6, существует обратный оператор к оператору (I-M),
который представляется в виде ряда Неймона:
-
ряд Неймона.
-
интегральный оператор, его ядро 
называется
итерированным ядром. Оно имеет следующий вид
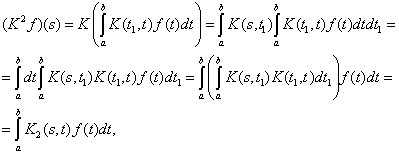
где 
- интерированное ядро.
.
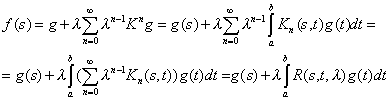Итак, получили решение
,
где 
называется резольвентой Фредгольма. Таким образом мы получили следующее
выражение для резольвенты Фредгольма
.
Если резольвента найдена, то дальнейшее
решение получается простым интегрированием. Такое представление резольвенты
называется рядом Неймана. Оно справедливо, только если 
.
В дальнейшем мы получим более общее представление для решения.