Опр.1
Опр. 2
Теорема
6.2. Принцип сжимающих отображений
Ряд вопросов, связанных с существованием и единственностью решений уравнений того или иного типа (например, дифференциальных или алгебраических уравнений), можно сформулировать в виде вопроса о существовании и единственности неподвижной точки при некотором отображении соответствующего метрического пространства в себя. Среди различных критериев существования и единственности неподвижной точки при такого рода отображениях один из простейших и в то же время наиболее важных – так называемый принцип сжимающих отображений.
Отображение A метрического пространства
M в себя называется сжимающим отображением (сжатием), если
существует такое число 
,
что для любых двух точек 
выполняется
неравенство
  . |
(1) |
Точка x называется неподвижной точкой отображения A, если Ax=x. Иначе говоря, неподвижные точки – это решения уравнения Ax=x.
Теорема. (Принцип сжимающих отображений).
Всякое сжимающее отображение, определенное в полном метрическом пространстве M, имеет одну и только одну неподвижную точку.
Доказательство.
Пусть 
-произвольная точка в M. Положим 
Покажем, что последовательность 
фундаментальная. Действительно, считая для определенности 
,
имеем
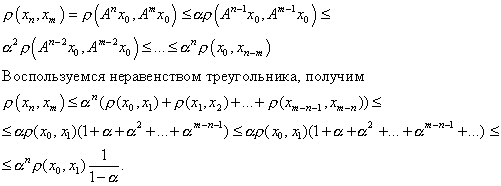
Так как ,
то при достаточно большом n эта величина сколь угодно мала. В силу
полноты M последовательность ,
будучи фундаментальной, имеет предел.
Положим 
.
Если 
,
то в силу (1) 
.
Поэтому
.
Итак, существование неподвижной точки доказано. Докажем ее единственность.
Если 
,
то (1) принимает вид
.
Так как ,
отсюда следует, что
.
Теорема доказана.
Пример.
6.2.1. Пусть f – функция, определенная на отрезке [a,b] и удовлетворяющая условию Липшица
с константой K<1. Пусть f отображает отрезок [a,b] в себя. Тогда f есть сжимающее отображение и, согласно доказанной теореме, последовательность
сходится к единственному корню уравнения
.
В частности, условие сжимаемости выполнено, если функция дифференцируема
и 
.
- получили одно решение в точке 0, так как в точке 1 нарушается сжимаемость, т.е. замкнутое изображение не сжимающее.
Сжимаемости нет, так как при каждой итерации расстояние увеличивается.