5. Решение ряда физических задач
5.1. Метод подобия
Для решения ряда
задач теплопроводности весьма полезен метод подобия.
Функция источника для бесконечной
прямой.
Будем искать решение уравнения теплопроводности
  |
(1) |
с начальными условиями
 . |
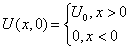(2) |
Уравнение теплопроводности остается неизменным при преобразовании переменных
 |
раз.
При указанном изменении масштабов
начальное условие (2) остается также без изменения, поэтому для функции
должно
иметь место равенство
 , |
при любых значениях x, t и k.
Для решения выберем новую переменную, которая не меняется при указанном преобразовании:
 |
Будем искать решение в виде:
.
Вычисляя производные U,
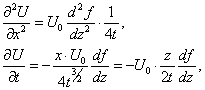
подставляя в уравнение (1) и сокращая
на множитель 
,
приходим к обыкновенному дифференциальному уравнению:
делаем замену переменной 
.
Проинтегрируем обе части уравнения
.
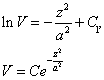
Необходимо определить пределы интегрирования:
так как t в знаменателе, а в начальном условии (2) t=0,
имеем:
1). 
.
при
 |
(3) |
2). 
 . |
(4) |
Итак,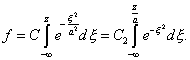 
Здесь нижний предел выбран так, чтобы выполнялось условие (4). Чтобы удовлетворить условию (3), следует положить:
.
Таким образом,
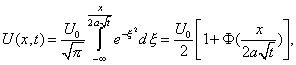
где
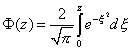-интеграл
ошибок.