5.2. Задача без начальных условий
Если изучается процесс теплопроводности в момент, достаточно удаленный от начального, то влияние начальных условий практически не сказывается на распределении температуры в момент наблюдения.
Рассмотрим задачу для полубесконечного стержня:
найти ограниченное решение уравнения теплопроводности в области x>0,
  |
(1) |
удовлетворяющее условию
 . |
(2) |
Это наиболее часто встречающийся случай граничного условия взадачахоб установившемся тепловом режиме.
Заменим граничное условие (2) на
 . |
(2*) |
Из линейности и вещественности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же уравнению.
Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2*), то его действительная часть удовлетворяет условию (2),
,
а мнимая – условию
.
Нужно найти установившийся режим при большом значении t.
Решение будем искать в виде
 , |
(3) |
где 
и 
- неопределенные пока постоянные.
Подставим выражение (3) в уравнение (1) и граничное условие. Находим
Подставим полученные значения
и
в уравнение (3)
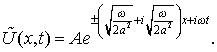
Для нахождения 
необходимо взять вещественную часть от 
:
 |
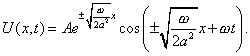(4) |
Это решение удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (4) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде
