Теорема

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.2. Теорема единственности для уравнения теплопроводности

Если две функции, определенные и непрерывные в области , удовлетворяют уравнению теплопроводности с начальными и краевыми условиями

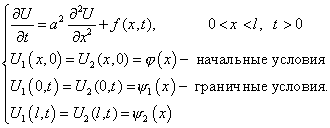(1)

то

Рассмотрим функцию Функция V(x,t) является решением однородного уравнения теплопроводности в этой области (o<x<l, t>0).

.
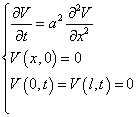Надо доказать, что однородное уравнение с однородными условиями имеет только тривиальное (то есть равное нулю) решение. Для доказательства будем использовать принцип максимума
( минимума ). Докажем его.

Принцип максимума ( минимума ) :

Если функция , определенная и непрерывная в замкнутой области и , удовлетворяет уравнению теплопроводности

(2)

в точках области , то максимальное и минимальное значения функции достигаются или в начальный момент, или в точках границы x=0 или x=l.

Доказательство (от противного)

Обозначим через M максимальное значение

при или

при

и допустим, что в некоторой точке функция достигает своего максимального значения, равного

Сравним знаки левой и правой частей уравнения (8) в точке . Так как в точке функция достигает своего максимального значения, то
и (3)

Так как достигает максимального значения при , то

. (4)
Сравнивая знаки правой и левой части уравнения (2), мы видим, что они различны. Однако это рассуждение еще не доказывает теоремы, так как правая и левая части могут быть равны нулю, что не влечет за собой противоречия.
Для полного доказательства найдем точку , в которой и . Для этого рассмотрим вспомогательную функцию
(5)

где - некоторое постоянное число. Значит, функция V(x,t) не является решением уравнения теплопроводности. Очевидно, что

Выберем так, чтобы был меньше то есть тогда максимальное значение при или при, не будет превосходить , то есть

(при t=0 или x=0, или x=l), (6)

так как для этих аргументов первое слагаемое формулы (5) не превосходит

а второе .

В силу непрерывности функции она должна в некоторой точке достигать своего максимального значения.

Очевидно, что

Поэтому и так как при или , имеет место неравенство (6). В точке , по аналогии с (4) и (5), должно быть

Учитывая (6), находим:

Отсюда следует, что

то есть уравнение (2) во внутренней точке не удовлетворяется. Тем самым доказано, что решение уравнения теплопроводности (2) внутри области не может принимать значений, превосходящих наибольшее значение на границе (т. е. при ).

Докажем единственность. Максимум и минимум достигается на границе, а следовательно, решение единственное

ФункцияV(x,t) достигает своего максимального значения или при t=0, или при x=0, илипри x=l. Однако, по условию мы имеем:

V(x,0)=0, V(0,t)=0, V(l,t)=0.

Поэтому
Теорема доказана.
  назад главная страница вперед