Фазовая плоскость.

Для выявления характера решения (9) удобно воспользоваться плоскостью состояний (x,t) или “фазовой плоскостью”. Прямые x-at=const и x+at=const называются характеристиками уравнения (1). Функция U=f(x-at) вдоль характеристики x-at=const сохраняет постоянное значение, функция U=f(x+at) постоянна вдоль характеристики x+at=const.
Рассмотрим некоторую фиксированную точку и проведем из нее обе характеристики и , которые пересекают ось X в точках , t=0 и , t=0.
ΔMPQ называется характеристическим треугольником точки .
Из формулы (9) видно, что отклонение U точки струны в момент времени зависит, только от значений начального отклонения в вершинах, P и Q треугольника ΔMPQ, и от значений начальной скорости на стороне PQ.
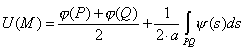. (10)
Начальные данные, заданные вне PQ, не оказывают влияния на значения U(x,t) в точке M. Если начальные условия заданы не на всей бесконечной прямой, а на отрезке , то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок .
Решение (9) можно представить в виде суммы
, (11)
  где
 

Наглядное представление о характере процесса распространения можно получить с помощью фазовой плоскости (x,t). Проведем характеристики через точки (a,0) и (b,0) они разбивают
плоскость (-∞<x<∞, t≥0) на шесть областей (рис.4). Отклонение в любой точке (x,t) дается
формулой (11).

Рассмотрим два случая:
1). Пусть на отрезке [a,b].
Если начальная скорость равна нулю, то отклонение есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 0,5φ(x), равной половине начального отклонения.
I,V - колебаний нет;
II -волна движется налево;
IV -волна движется направо;
VI – две волны;
III – колебаний нет, отклонение равно нулю.

2). Пусть на отрезке [a,b].

Если начальное отклонение равно нулю, то представляет возмущение струны, создаваемое начальной скоростью.

I, V – нет колебаний и отклонений;
II -волна “бежит” налево с изменением формы;
IV 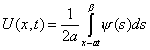-волна “бежит” направо с изменением формы;
VI – две волны;
III 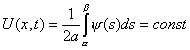-колебаний нет, но струна не возвращается в исходное положение. (если постоянная не равна нулю).

 

 

 

 

 

 

 

 

 

 

 

 

 

 
<<назад главная страница вперед>>