4.2 Статистические характеристики когерентных изображений нескольких точек при дискретном спектре подсвечивающего излучения

В реальных условиях подсвечивающее объект излучение никогда не бывает чисто когерентным. Оно может состоять из дискретного или непрерывного набора волн (частот), что приводит к ухудшению временной когерентности излучения. Рассмотрим влияние излучения в виде набора дискретных волн на статистические характеристики изображения.

Изображения, получаемые при фотографировании в белом свете, не имеют пятнистой флуктуационной структуры. Поэтому, можно предположить, что с увеличением числа длин волн подсвечивающего излучения контраст в изображении будет уменьшаться.

Пусть объект состоит из двух случайно расположенных точек, и в подсвечивающем излучении присутствуют две длины волны. В этом случае ,

где

Следовательно, интенсивность изображения представляет собой меняющуюся со временем структуру с периодом изменения .

Разность частот излучения w₂ - w₁ для оптического диапазона волн обычно велика. Даже при отличии длин волн на 10^-5 % она составляет порядка 10 МГц. Характерное время регистрации оптических изображений 10^-7 с и выше. Следовательно, регистрироваться будет усредненная по времени интенсивность - плотность энергии излучения

,

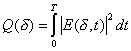где T – время регистрации изображения.

В этом случае имеет смысл говорить о статистических характеристиках величины Q(d  ).

Для объекта из двух точек после интегрирования по t

,

где .

При TDw>>1, Q(d  )=(I₁ + I₂)T.

Тогда

.

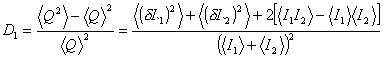Следуя результатам предыдущего параграфа, имеем:

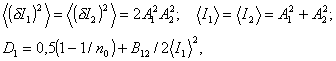
где - частотная корреляционная функция.

Учитывая, что , получаем

.

Предположим, что z₁ – z₂ распределено по гауссовскому закону с . Тогда после усреднения получим

.

Для случая, когда z₁ – z₂ распределено по равномерному закону в интервале (-h_m/2, h_m/2 .

Если (w₁ - w₂)s/c>>1, (w₁ - w₂) h_m /c>>1, то D₁ = D/2. В противоположном случае D₁» D. Это значит, что контраст при подсвете двухточечного объекта двумя достаточно разнесенными длинами волн падает в два раза. При слабом разнесении длин волн падение контраста отсутствует.

Например, при s = 100l разнесение по длинам волн, приводящее к двукратному падению контраста, составляет Dl=l ²/s » 10^-2 l.

При Dl << 10^-2 l падение контраста не происходит.

С физической точки зрения падение контраста в изображении при подсвете объекта сильно разнесенными длинами волн объясняется тем, что в плоскости изображения формируются два или несколько несовпадающих между собой изображения.

Двукратное падение контраста при (w₁ - w₂)s /   c>>1 имеет место и при подсвете многоточечного объекта.

Рассмотрение случая, когда многоточечный объект подсвечивается несколькими длинами волн l_m = 2pc/w_m , m = 1,2, … , m₀ приводит к D₁ = D/m₀ при (w_m - w_n)s/ c>>1. В противоположном случае D₁ = D, т. е. контраст такой же, как при подсвете многоточечного объекта одной длиной волны.

Таким образом, контраст в изображении многоточечного объекта со случайным расположением точек меняется от контраста D, получаемого на одной длине волны, до контраста D/m₀, имеющего место при условии, что все длины волн удовлетворяют неравенствам

,

где m₀ – кратное падение контраста является следствием сложения m₀ статистически независимых изображений, получаемых на различных длинах волн. Это приводит к m₀ – кратному уменьшению относительной дисперсии суммы этих изображений.

При рассмотрении данного вопроса мы не учитывали корреляционных связей между точками, которые имеют место, если объект непрерывен, не учитывалось также интенсивности каждой из спектральных составляющих и форма объекта.

В случае эквидистантного расположения длин волн облучения относительно l, результату

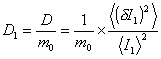можно дать следующую интерпретацию. Пусть Dl - ширина спектра излучения. Тогда интервал между соседними длинами волн составляет величину Dl/m₀. Условие статистической независимости изображений, получаемых на соседних длинах волн .

Отсюда , где - параметр, описывающий длину когерентности излучения. Следовательно, .

Физический смысл последнего выражения состоит в том, что контраст в изображении, получаемом на широком спектре длин волн, падает во столько раз по сравнению с контрастом изображения, получаемом на одной длине волны, во сколько раз длина когерентности излучения меньше дисперсии расстояния между точками объекта. Этот результат есть следствие того факта, что при l_c<<s расстояния между точками объекта столь велики, что их можно мысленно разбить на участки вдоль оси z, причем эти участки (даже соседние) будут рассеивать излучение, не интерферирующее друг с другом. Число таких статистически независимых полей как раз и составляет m₀ = l_c/s.

Качественно подобная картина будет иметь место и при произвольном виде спектра. В этом случае Dl - полуширина спектра, .

---