4.3 Статистические характеристики изображения объекта при его движении и монохроматическом подсвете с разных направлений

Пусть многоточечный неподвижный объект подсвечивается одновременно с нескольких направлений; источники подсвета расположены в плоскости апертуры линзы, формирующей изображение; начальные фазы излучения источников случайны и независимы.

Двухточечный объект. ,

где E_иs – амплитуда поля j – го источника на объекте, q_s – углы падения, s = 1, 2, sinq_s = r_иs/êr_ц - r_иs ê, r_иs – положение источников, y_s – начальные фазы источников. Очевидно, <E₁E^*₂>_и = 0, где < >_и – усреднение по фазам источников. С учетом этого условия контраст в изображении равен ,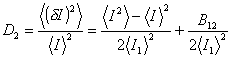

где

После усреднения по фазам j₁, j₂ получим при E_и1 = E_и2 = E_и

.

Отсюда

.

При q₁ = q₂ имеем D₂ = D; при получим D₂ = D/2.

При A₁ ¹ A₂ <E₁E^*₂> не обращается в нуль. Таким образом, D₂ является периодической функцией. Двукратное падение контраста объясняется периодической декорреляцией интенсивностей в изображении при изменении угла подсветки q₂.

Многоточечный объект.

Поле в изображении

где ,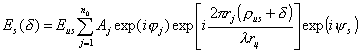

где r_иs – радиус-вектор s – го источника; n₀ – число точек объекта, y_s – фаза источника, m₀ – число источников.

Тогда средняя интенсивность в изображении равняется

,

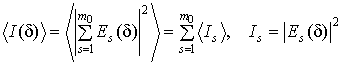где < > - усреднение по источникам и по фазам j_j, обусловленным случайным расположением точек.

В случае независимых точек объекта.

,

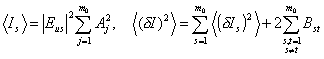где.

Вычислим величину B_st. Так как при конечном числе точек объекта E_s распределено не по гауссовому закону, то, вообще говоря, B_st ¹ ê<E_sE^*_t> ê², что уже было видно на примере двухточечного объекта.

В случае конечного числа объектов n₀, нетрудно показать, что с точностью до несущественных множителей при n₀ ® ¥ получим

,

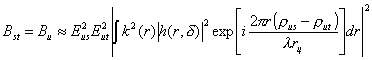где интегрирование проводится по поверхности объекта. Отсюда для линзы квадратной формы при хорошем разрешении можно получить

B_и » 0 при êr_иs - r_иt ê>d_r.

Следовательно, при разнесении источников подсвета объекта на расстояние, большее размеров апертуры линзы d_r, наступает полная декорреляция между изображениями. С физической точки зрения это объясняется тем, что при изменении направления подсвета объекта поле также поворачивается относительно объекта, но в противоположном направлении.

При повороте поля на угол d_r  / r_ц происходит полная смена одной реализации поля на апертуре линзы на другую реализацию. Это приводит к эффекту декорреляции интенсивностей изображений, получаемых до и после поворота источника подсвета на угол d_r  / r_ц. Следует отметить, что поворот поля по законам зеркального отражения имеет место лишь при n₀ ® ¥. В этом случае многоточечный объект трансформируется в объект со сплошной поверхностью, отражающей по законам, близким к геометрической оптике.

В случае объекта, состоящего из малого числа точек, функция корреляции интенсивностей B₁₂ в изображении не стремится к нулю при изменении направлении подсвета. Для двухточечного объекта она даже периодическая. Это связано с тем, что при изменении направления подсвета подобного объекта законы геометрической оптики не выполняются даже приблизительно.

Учитывая соотношение для функции корреляции интенсивностей B_st и, полагая, что амплитуды источников равны, а, следовательно, найдем контраст изображения, получаемого при подсвете от независимых источников

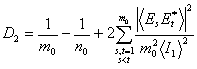, при s = t, D₂ = 1 – 1/n₀ = D.

Таким образом, при совпадении источников, контраст, естественно, сохраняется прежним, как и при подсвете из одного источника. В случае конечного числа m₀ и при достаточно большом числе точек n₀, составляющих объект происходит декорреляция полей, т.е. . В этом случае D₂ » 1/m₀. Этот результат является следствием наложения m₀ изображений с независимыми полями, что, как известно, приводит к m₀-кратному падению контраста. Исходный единичный контраст принят в силу предположения, что n₀ ®¥. Условие декоррелируемости полей состоит в том, чтобы источники были разнесены между собой на расстояния . По аналогии со случаем подсвета объекта различными длинами волн, при котором падение контраста в изображении наступает при условии , можно переписать условие в виде , где l_п – длина пространственной когерентности источников, равная d_r.

Таким образом, контраст при подсвете объекта источниками со случайными и независимыми за время наблюдения фазами, что имеет место, например, из-за изменения взаимного расположения источников, с ростом числа подобных источников уменьшается. Такие источники принято считать некогерентными между собой.

Рассмотрим случай, когда источники расположены внутри области, равной половине апертуры линзы. Для упрощения анализа, расположим их по одной линии, и будем считать, что n₀®¥. В этом случае

,

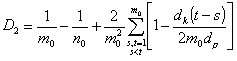где d_k – расстояние между крайними источниками. Тогда после суммирования по s и t получим

.

При m₀ >> 1, D₂ = D – d_k / 6d_r (d_k < d_r / 2  по условию), D = 1 – 1/n₀.

Контраст суммарного изображения в этом случае превышает D - 0.1. При уменьшении максимального расстояния между источниками d_k контраст D₂ возрастает и при d_k ®0 стремится к D независимо от числа источников. Рост размеров апертуры линзы также приводит в этом случае к возрастанию контраста.

К уменьшению контраста приводит также изменение фазовых набегов между соседними точками при изменении направления подсвета объекта.

---