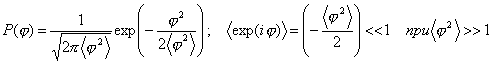4 ТЕОРИЯ КОГЕРЕНТНЫХ ИЗОБРАЖЕНИЙ

4.1 Статистические характеристики когерентных изображений. Контраст изображения

Рассмотрим свойства когерентного изображения для случая, когда объект подсвечивается когерентным излучением, и состоит из двух точечных объектов. Зададим расположение этих объектов с помощью радиус-векторов r₁=(x₁, y₁, z₁), r₂=(x₂, y₂, z₂). И пусть изображение этого объекта строится тонкой линзой в плоскости, отстоящей от нее на расстоянии z_и. Пусть z₁»  z₂»  r_ц, причем

êz₁ – z₂ ê<<l  r_ц ² ¤ dd_r,

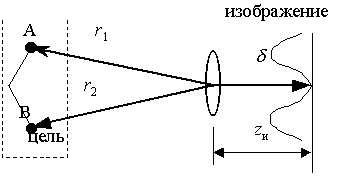
Рис. 48. Формирование изображения двухточечного объекта

где d_r - минимальный линейный размер апертуры линзы, d – максимальный линейный размер объекта (расстояние от оси z до наиболее удаленной от нее точки объекта).

Линза, формирующая изображение, имеет фокусное расстояние f: 1/f=1/r_ц+1/z_и. В этом случае поле в изображении представляется в виде сумм двух слагаемых:

,

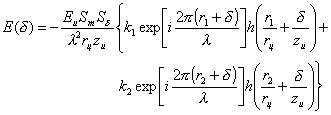где k₁, k₂ – коэффициенты отражения от точечных объектов, l - длина волны подсвечивающего излучения, r_ц – среднее расстояние от объекта до линзы, z_и – расстояние от линзы до изображения,

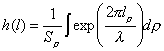
- импульсный отклик линзы, r - радиус-вектор апертуры линзы, - поле в плоскости объекта от источника, E₀ – амплитуда поля источника, S_и – площадь источника, r_и – радиус вектор источника, d - радиус вектор изображения, S_r - площадь апертуры линзы, S_Т – сечение рассеяния точечного объекта. Интегрирование производится по апертуре линзы.

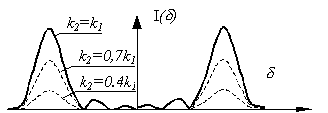
Рис. 49. Распределение интенсивности в когерентном изображении двухточечного объекта

На рис. 49 приведены построенные при различных x₁, x₂ реализации изображений для плоского случая. Видно, что распределение интенсивности   I (d  ) = ï ;E(d  )ï   ² существенно зависит как от k₁, k₂, так и от функции h(l) и x₁, x₂. Естественно считать k₁»  k₂. Если выполняется условие x₁- x₂ < l  r_ц /d_r, то при k₁ » k₂ отклики от обоих точечных объектов располагаются практически в одном месте.

Представим далее, что расположение точечных объектов случайно и величина z₁ - z₂ имеет определенный (например, гауссовский или равномерный) закон распределения.

Введем обозначения ;

.

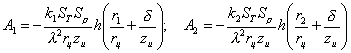Тогда

.

Пусть фаза j = j₁ - j₂ распределена по закону Р(j) с шириной j₀, характеризующей разброс фазы j. Обычно j₀ >>2p, Р(j)®0 при j®±¥.

Исходя из этих условий, нетрудно показать, что

,

где < > - операция усреднения.

В частности, при гауссовском законе распределения

При равномерном законе распределения

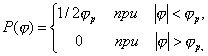
где j_p ширина распределения; .

Используя последнее соотношение с учетом независимости точек, получим для дисперсии , и для среднего значения интенсивности . Отсюда относительная дисперсия равна

.

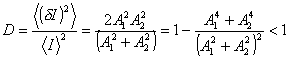Эта величина очень важна для характеристики изображения и часто называется контрастом. Чем меньше D, тем более равномерна яркость изображения, меньше отличаются его наиболее темные и светлые места. В данном случае максимальное значение контраста D = 0,5 и достигается при A₁=A₂.

Уже из анализа этого случая видно, что когерентные изображения объектов, состоящих из точек с достаточно большим случайным разбросом расстояний между ними, сильно флуктуируют, т.е. представляют собой сильно изрезанные по яркости структуры. И можно предположить, что при увеличении числа точек, составляющих подобные объекты, контраст будет увеличиваться.

Обобщим полученный результат на случай, когда объект состоит из n₀ независимо расположенных точек. В этом случае

.

Очевидно, j_j независимы, т.е. их совместный многомерный закон распределения распадается на произведение одномерных распределений:

.

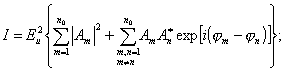
Раскрывая это соотношение получим:

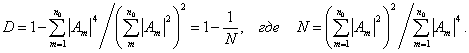
Из последнего соотношения видно, что при n₀ >>1, D » 1, т.е. контраст в когерентном изображении многоточечного объекта, состоящего из случайно и независимо расположенных точек, разброс по фазе которых существенно превышает длину волны подсвечивающего излучения, стремится к единице.

Для объекта, состоящего из большого числа точек, достаточно общие результаты могут быть получены следующим путем. По центральной предельной теореме теории вероятностей вещественная и мнимые части поля в изображении многоточечного объекта со случайным и независимым расположением точек должны приближенно описываться гауссовскими распределениями, так как они представлены в виде суммы большого числа независимых слагаемых. Непосредственным вычислением легко убедиться, что вещественная часть поля и мнимая часть имеют одинаковые дисперсии и нулевую корреляцию . Следовательно, при большом n₀ они будут представлять собой две одинаково распределенные и независимые гауссовские величины. Интенсивность изображения будет экспоненциально распределенной величиной. Для экспоненциального распределения , т.е. контраст много точечного изображения D »1.

Можно показать, что близость распределения к гауссовскому как раз следует из приблизительного равенства контраста D единице.

---