2 КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ И КОГЕРЕНТНОСТЬ
2.1 Распространение взаимной когерентности.
Распространение световых волн, функция
взаимной когерентности
Пусть u(P,t) - скалярная амплитуда одной компоненты поляризации
электрического или магнитного поля, связанная с монохроматическим оптическим
сигналом (излучением). В соответствии с принятым в скалярной теории подходом,
рассмотрим каждую компоненту независимо. Здесь Р - пространственная координата точки, а параметр t - момент времени. Аналитический сигнал, связанный с u(P,t), имеет
вид 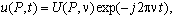 где n -
частота волны, а U(P,n)
- амплитуда фазора.
где n -
частота волны, а U(P,n)
- амплитуда фазора.
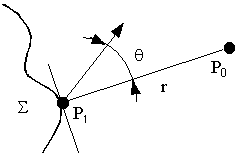
Рис.6. Схема распространения излучения
Пусть волна падает слева на неограниченную поверхность. Необходимо найти амплитуду фазора поля в точке Ро справа от поверхности S через характеристики поля на поверхности S.
В соответствии с принципом Гюйгенса-Френеля справедливо следующее решение
 ,
,
где l = с /n - длина волны излучения (с - скорость света); r - расстояние от точки Р1 до точки Р0; q - угол между прямой линией, соединяющей Р0 и Р1 , и нормалью к поверхности S; c(q) – коэффициент наклона, c(0) = 1 и 0 £ c(q) £ 1.
Как правило, рассмотрение большинства задач ведется в приближении малых углов наклона и поэтому в дальнейшем, мы будем считать этот множитель равным единице.
Принцип Гюйгенса - Френеля можно интерпретировать таким образом. Каждая точка на поверхности S действует как новый вторичный источник сферических волн. Напряженность поля вторичного источника в точке Р1 пропорциональна (jl)-1U(P1,n), и этот источник излучает с амплитудным коэффициентом направленности c(q).
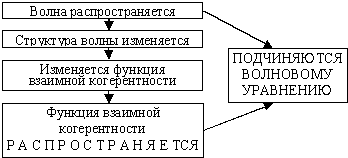
Рис.7. Распространение функции взаимной
когерентности
Функция взаимной когерентности. При распространении волны в пространстве ее структура изменяется. Изменяется соответственно и функция взаимной когерентности. Следовательно, можно говорить о распространении функции взаимной когерентности.
Причина
эта объясняется тем фактом, что световые волны подчиняются волновому уравнению.
Решение, основанное на
принципе Гюйгенса – Френеля. Рассмотрим распространение световой волны с произвольными свойствами когерентности. Дана функция взаимной
когерентности G(R1,R2;t)
на поверхности å1 и надо найти функцию взаимной когерентности Г(Q1,Q2;t)
на поверхности å2. То есть наша цель
предсказать результаты
интерференционного опыта Юнга на отверстиях Q1 и Q2 если известны
результаты интерференционных опытов на всевозможных отверстиях Р1
и Р2.
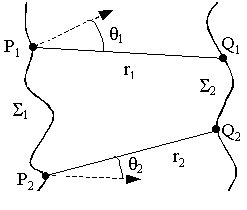
Рис.8. Процесс распространения функции взаимной
когерентности
По определению функция взаимной когерентности на поверхности å2
G(Q1,Q2;t) = < u (Q1 ,t + t)u*(Q2,t) > .
Используя выражение для распространения узкополосного сигнала
![]()
запишем
выражение для узкополосного сигнала для нашего случая для двух точек Q1 и Q2
поверхности S2![]()
![]()
![]()
![]()
![]() ,
,
Подставив выражение для
полей в функцию взаимной когерентности и изменяя порядок выполнения
интегрирования и усреднения, получим
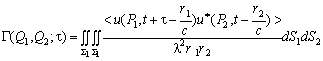 .
.
Среднее по времени в подынтегральном выражении может быть выражено через функцию взаимной когерентности на поверхности S1, что приводит к основному закону распространения взаимной когерентности
![]() .
.
В соответствии с условием квазимонохроматичности (Dw/w<<1) оптическая разность хода должна быть намного меньше длины когерентности излучения. Опираясь на это условие, найдем закон распространения излучения для взаимной интенсивности, заметив, что
![]() ; t=0,
; t=0,
а также
![]() .
.![]()
Подставив это в выражение для распространения взаимной когерентности, при t=0 получим
![]() .
.
Это основное выражение, определяющее
закон распространения взаимной интенсивности.
Распределение интенсивности на поверхности S2 можно найти, устремив Q1 к Q2 (т.е. точки Q1 и Q2 должны совпасть) в последней формуле и заменив
r1 ® r1¢, r2 ® r2¢, Q1 ® Q1¢ , Q2 ® Q2¢ .