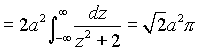|
|
|
|
|
||
2.6.1.с. Вычисление площади сектора, ограниченного кривой, заданной в полярной системе координат.
Воспользуемся формулой для нахождения площади в полярной системе координат . Так как фигура симметрична относительно оси ОХ, будем брать интеграл только по половине промежутка: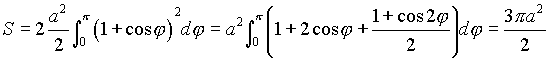
Используя симметрию фигуры относительно оси ОУ, будем искать половину площади. Сначала, рассматривая уравнения заданных кривых как систему двух уравнений, найдем значение ![]() , при котором кривые пересекаются:
, при котором кривые пересекаются: 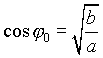 . (Значение корня взято со знаком +, так как угол лежит в первой четверти.)
. (Значение корня взято со знаком +, так как угол лежит в первой четверти.)
Требуемую площадь найдем как разность S1 -площади треугольника, ограниченного лучем ![]() , прямой
, прямой 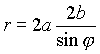 и осью ОУ и S2 -площади сектора, ограниченного лучем
и осью ОУ и S2 -площади сектора, ограниченного лучем ![]() и кривой
и кривой 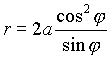 .
.
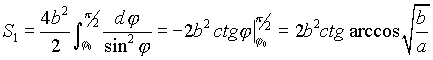
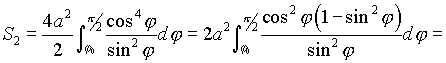
=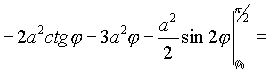
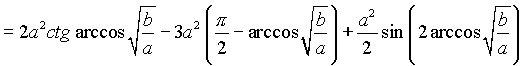
Таким образом, искомая площадь будет равна 2(S1 - S2 ).
Элементарными преобразованиями ответ может быть приведен к виду 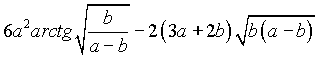
Перейдем к полярной системе координат: ![]() . Тогда уравнения данных кривых будут иметь вид
. Тогда уравнения данных кривых будут иметь вид ![]() и
и ![]() . Решая систему этих уравнений относительно
. Решая систему этих уравнений относительно ![]() , получим значения переменной
, получим значения переменной ![]() в точках пересечения этих кривых:
в точках пересечения этих кривых: 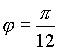 и
и 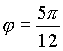 . Искомая площадь будет
. Искомая площадь будет 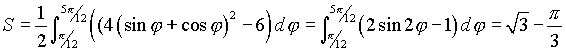
Перейдем к полярной системе координат: ![]() . Уравнение данной кривой будет
. Уравнение данной кривой будет ![]() . Так как кривая симметрична относительно как оси ОХ, так и оси ОУ, то, используя формулу для вычисления площади в полярной системе координат , найдем сначала четверть искомой площади:
. Так как кривая симметрична относительно как оси ОХ, так и оси ОУ, то, используя формулу для вычисления площади в полярной системе координат , найдем сначала четверть искомой площади: 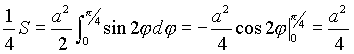
Перейдем к полярным координатам по формулам ![]() . Тогда уравнение данной кривой будет
. Тогда уравнение данной кривой будет 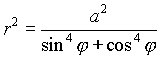 . Так как фигура симметрична как относительно оси ОХ, так и оси ОУ, то можно брать интеграл только по четверти промежутка и искомая площадь будет
. Так как фигура симметрична как относительно оси ОХ, так и оси ОУ, то можно брать интеграл только по четверти промежутка и искомая площадь будет 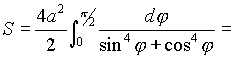
Преобразуем подынтегральную функцию и сделаем подстановку ![]()
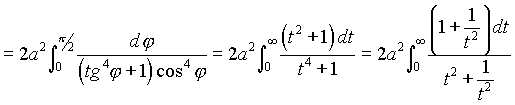 =
=
Теперь сделаем замену переменной 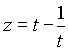 :
: