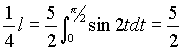|
|
|
|
|
|
||
2.6.2.а. Решения
1. Воспользуемся формулой для вычисления длины дуги, заданной параметрически.
Найдем производные от функций, задающих кривую: 
. Тогда 
и длина дуги будет равна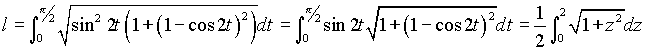 
(здесь сделана замена переменной 
).
Последний интеграл вычислим по частям:
=
= 
.
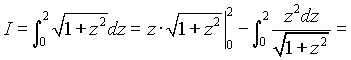
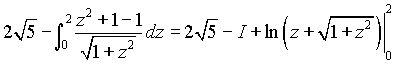Рассматривая это равенство, как уравнение относительно I, получим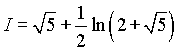 
и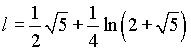 
2. Воспользуемся формулой для вычисления длины дуги, заданной параметрически.
Найдем значения параметра, при которых 
. Для этого решим неравенство 
. Имеем: 
. Тогда 
.
Теперь вычислим подынтегральное выражение: 
.
Таким образом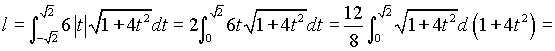 
.
При вычислении интеграла использовано свойство 6 аддитивности интеграла по промежутку
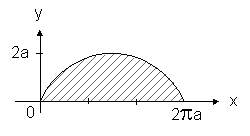
Воспользуемся формулой для вычисления длины дуги, заданной параметрически.
Сначала вычислим подынтегральное выражение: 
Теперь найдем длину дуги циклоиды между двумя произвольными точками, лежащими на ее первой арке: 
, где 
- произвольные значения t на промежутке 
.
Полагая 
, получим длину всей циклоиды: 
.
Очевидно, что части циклоиды, лежащие под прямой y=c, будут равны, поэтому, если - значения параметра, соответствующие точкам пересечения циклоиды и этой прямой, то 
. Учитывая этот факт, найдем такое значение 
, чтобы длина части арки циклоиды, лежащей над прямой y=c, была бы равна 1/3 от длины всей арки: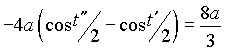 
. Так как 
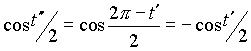, то получим 
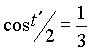и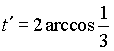 
. Подставляя это значения в уравнения кривой, найдем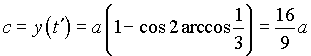 
Теперь воспользуемся формулой для вычисления длины дуги пространственной кривой, заданной параметрически: 
5. Воспользуемся формулой для вычисления длины дуги, заданной параметрически.
Для этого вычислим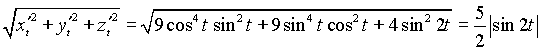 
Так как период подынтегральной функции равен 
, то, вычисляя интеграл по промежутку 
, получим четверть искомой длины: 
.