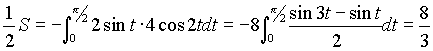|
|
|
|
|
||
2.6.1.b Решения
1. Данные параметрические уравнения задают эллипс.
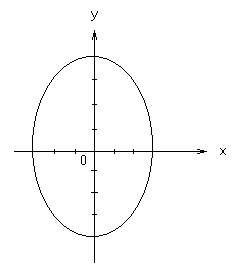
Так как эта фигура симметрична относительно каждой из координатных осей, то будем считать четверть искомой площади: 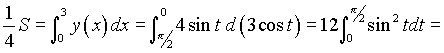
=![]()
2. Обозначим через x1 наибольшее значение переменной x на данной кривой и через t1 значение параметра t, при котором x=x1.
Тогда площадь можно вычислить как разность двух площадей: ![]() , где y2 - функция, задающая верхнюю часть петли, а y1 - функция, задающая нижнюю часть петли на промежутке
, где y2 - функция, задающая верхнюю часть петли, а y1 - функция, задающая нижнюю часть петли на промежутке ![]() . Отметим, что петля начинается в начале координат при t=0 и заканчивается там же при t=3. Поэтому, переходя в указанных интегралах к переменной t, получим
. Отметим, что петля начинается в начале координат при t=0 и заканчивается там же при t=3. Поэтому, переходя в указанных интегралах к переменной t, получим ![]() так как
так как ![]() на промежутке [t1 ,3] и
на промежутке [t1 ,3] и ![]() на промежутке [0,t1 ]. Вычисляя указанный интеграл, получим
на промежутке [0,t1 ]. Вычисляя указанный интеграл, получим 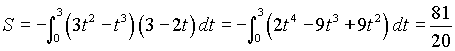
3. Петля данной кривой начинается в начале координат при t=0 и заканчивается там же при ![]() .
.
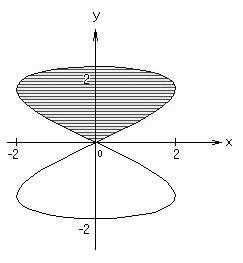
Но так как она симметрична относительно каждой из координатных осей, можно вычислять половину площади, которая получится, если параметр t пробежит интервал от 0 до ![]() .
.
Обозначим через x1 наибольшее значение переменной x на данной кривой и через t1 значение параметра t, при котором x=x1. Тогда площадь можно вычислить как разность двух площадей: ![]() , где y2 ? функция, задающая верхнюю часть петли, а y1 - функция, задающая нижнюю часть петли на промежутке
, где y2 ? функция, задающая верхнюю часть петли, а y1 - функция, задающая нижнюю часть петли на промежутке ![]() . Переходя в указанных интегралах к переменной t, получим
. Переходя в указанных интегралах к переменной t, получим ![]()
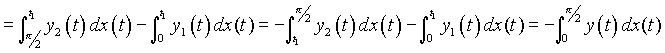 так как
так как ![]() на промежутке [t1 ,
на промежутке [t1 ,![]() ] и
] и ![]() на промежутке [0,t1 ]. Вычисляя указанный интеграл, получим
на промежутке [0,t1 ]. Вычисляя указанный интеграл, получим