	Уровень:

Интеграторы

Интегратор и дифференциатор - это две схемы из числа наиболее важных аналоговых вычислительных схем. Интегратор используется в схемах управления во всех тех случаях, когда надо решать дифференциальное уравнение или надо вычислить интеграл напряжения. Дифференциатор используется тогда, когда надо получить выходной сигнал, пропорциональный скорости изменения входного.

Интегратор.

Интегрирующие цепи предназначены для интегрирования во времени электрических входных сигналов. Величина входного сигнала в общем виде описывается уравнением

U_вх(t)= U_вых(0) + K

U_вx(t)dt, U_вых(0) - начальное значение выходного сигнала в момент времени t = 0, К - коэффициент пропорциональности.

Простейшей пассивной линейной интегрирующей цепью является чeтыpexпoлюcник, состаящий из RC - элементов.

Рис. 2.5

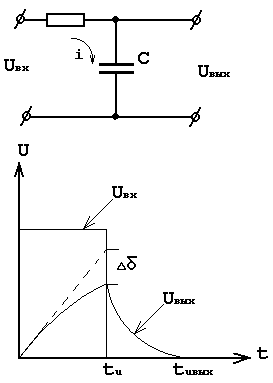
При подаче прямоугольного импульса с идеальными фронтами на интегрирующую RC цепь выходное напряжение нарастает по экспоненциальному закону: , где t=RC.

Используя разложение функции в ряд Маклорена получим

U_вых(t) = U_вx[ l^-l+l/t -1/2! (t/t)²+...+l/n(t/t)ⁿ]

Ограничившись первыми тремя членами разложения, получим

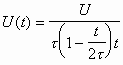
Первый член описывает U_вых(t) при идеальном интегрировании, второй - значение ошибки интегрирования. Эта ошибка имеет наибольшее значение при t = t_и

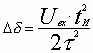
К моменту окончания импульса выходное напряжение достигает значения

U_вых(t)= U_вхt_и/t (1-t_и/2t), а затем по экспоненциальному закону убывает до нуля с постоянной времени t.

Следовательно, простейшие RC-цепочки мало применяют для точного интегрирования входных сигналов.

Окончательная погрешность интегрирования при t = t_и

= d / (U_вхt_и/t) = t_и/2t

Схема простейшего интегратора на ОУ:

Рис. 2.6

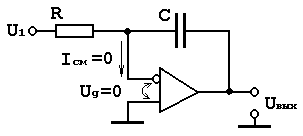
, где Q - электрический заряд, U - напряжение, т.е. Q = CU и изменяя заряд за единицу времени, то есть ток через конденсатор равен

Если ОУ близок к идеальному, то I_r= I_c, тогда

Так как U_д= 0, и U_c= - U_вых, можно написать

Решая это выражение относительно dU_вых, находим

, а интегрируя его получим

Примеры интегрирования.

Подадим на интегратор ступенчатый сигнал:

Рис. 2.7

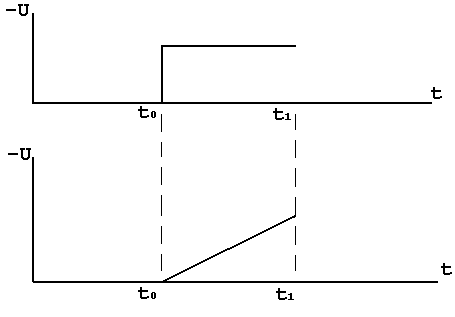
Входной ступенчатый сигнал как функция времени, т.е. U₁= U при t >= t₀, U₁= 0 при t > t₀, тогда

Изменение выходного напряжения во времени представляет собой наклонную прямую с полярностью входного сигнала.

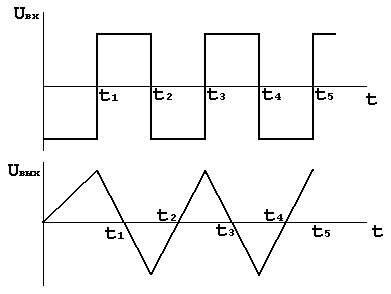
На вход интегратора подается сигнал прямоугольной формы

Рис. 2.8

Так как сигнал периодический, для описания выходного напряжения достаточно рассмотреть один полный период .

Выходной напряжение можно записать как функцию времени

После интегрирования получаем наклонную прямую на каждом полупериоде.

При любом сигнале на входе изменение сигнала на выходе должно начинаться от того значения, которое выходной сигнал имел к моменту прихода входного сигнала.

На вход интегратора подано пилообразное напряжение

, t₁< t < t₂, где

то есть напряжение на выходе - это квадратичная функция времени (парабола)

Рис. 2.9

Реальный интегратор

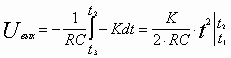
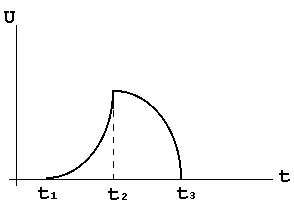
Реальный ОУ имеет некоторое напряжение сдвига и нуждается в некотором токе смещения. Напряжение сдвига интегрируется как ступенчатая функция, что дает дополнительный линейно-нарастающий (или падающий) выходной сигнал, полярность сигнала определяется полярностью U_сдв, а наклон величиной U_сдв. Ток смещения течет через конденсатор обратной связи, что также приводит к появлению наклонного выходного сигнала. Кроме того, U_сдв добавляется к напряжению на конденсаторе, и поскольку это напряжение равно U_вых, такая прибавка вносит в результат ошибку, равную U_сдв.

Выражение для U_вых примет вид

U_вых = -

+ U_сдвdt + I_смdt + U_сдв

Ошибку напряжения сдвига можно уменьшить следующими приемами :

использовать ОУ с низким U_сдв;
периодически сбрасывать интегратор;
шунтировать конденсатор С сопротивлением Rp.

Схема :

Рис. 2.10

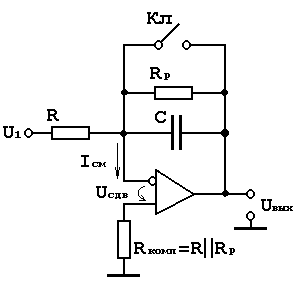
Резистор R_ком= R||R_p уменьшает ток смещения I_см.

Интегратор на ОУ эквивалентен обычной RC-цепи, у которой значение емкости конденсатора С увеличена в 1+К_оу, а падение напряжения на нем усилено в К_оу раз.

При подаче на вход импульса прямоугольной формы с постоянной величиной выходного напряжения

U_вых(t) = - U_вхK_oyt / [RC(l+K_oy)]

При подаче на вход интегратора на ОУ скачка напряжения выходной сигнал изменяется по экспоненциальному закону

U_вых(t)= - U_вхK_оу [l-exp( - t / t_c), где t_c=(l+K_oy)RC.

Относительная ошибка интегрирования

g = t_и/2t_с = t_и/[2(1+К_оу)RС

Т.о. погрешность интегрирования приблизительно в К_оураз меньше по сравнению с простой RC-цепыо при тех же номиналах RC.

АЧХ интегратора :

Рис. 2.11

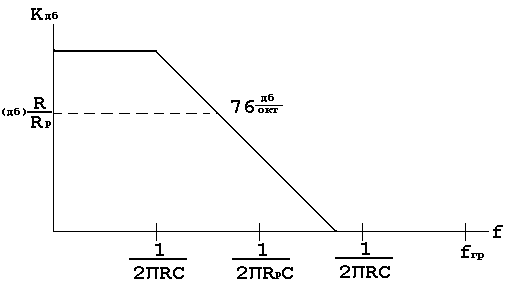
Частотная хaрaктеристика интегратора на полностью скорректированном по фазе ОУ.

Тонкая линия - хaрaктеристика интегратора без ОС, штриховая линия - характеристика интегратора при наличии R_p.

Для интегратора без резистора полоса частот, в которой происходит интегрирование, расположена между нижней сопрягающей частоте интегратора и частотой среза интегратора.

Частота среза F_ср =

Добавление сопротивления R_p- для улучшения стабильности на НЧ, при этом увеличивается сопрягающая (граничная) частота.

Нижняя граничная частота скорректированного интегратора составляет :

Fн = =

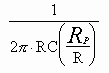Таким образом, полоса частот, в которой возможно интегрирование лежит между и частотой

Частотная характеристика стабилизированного по сдвигу интегратора (R_p включено) представляет собой частотную характеристику фильтра НЧ со спадом 6 дб/окт и с коэффициентом усиления, большим единицы.