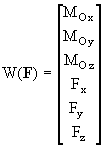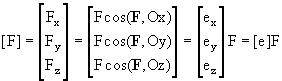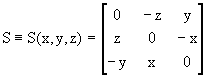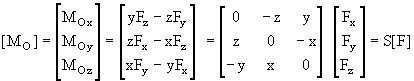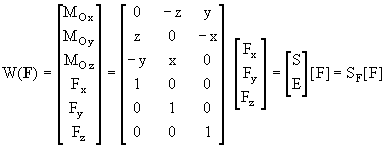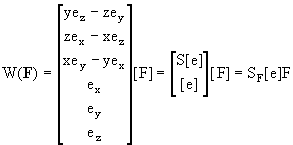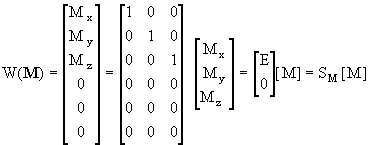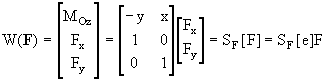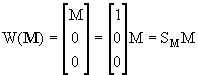Бивектором силы F относительно точки O будем называть столбцевую матрицу, составленную из осевых моментов и проекций этой силы:
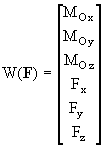
Столбцевую матрицу проекций силы будем обозначать [F]. Эта матрица может быть представлена произведением столбца проекций орта [e] (направляющих косинусов силы) на модуль силы F:
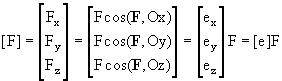
Введем кососимметрическую (3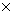
3) - матрицу, образованную из координат x,y,z точки приложения силы:
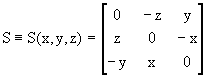
Тогда столбцевая матрица [MO], составленная из осевых моментов, выражается в виде произведения матрицы S и столбца [F]:
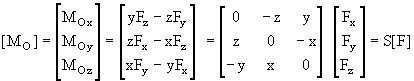
В результате бивектор силы можно определять как матричное произведение прямоугольной матрицы координат и столбцевой матрицы силы:
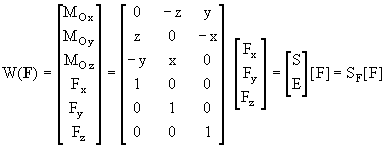
Здесь SF - прямоугольная (6 3) - матрица, состоящая из двух (3 3) - блоков: верхнего блока, равного матрице S и соответствующего "моментной" части бивектора, и нижнего единичного блока E, соответствующего его "силовой" части.
С использованием модуля и направляющих косинусов силы ее бивектор записывается в виде:
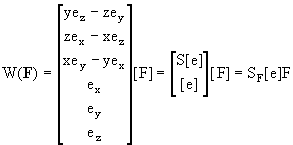
Бивектор пары сил с моментом M вычисляется по любой из следующих формул:
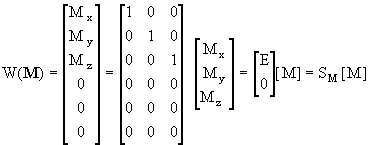
Здесь SM - прямоугольная (6 3) - матрица, состоящая из единичного и нулевого (3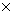 3) - блоков.
Если сила расположена в координатной плоскости Oxy, то среди шести компонент ее бивектора ненулевыми могут быть лишь Fx, Fy и MOz. Отбросив нулевые компоненты, получим выражение бивектора силы в виде:
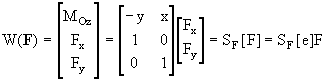
Парa сил, расположенная в плоскости Oxy, с моментом M, параллельным оси Oz, характеризуется бивектором
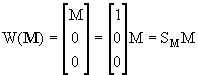
В последних двух матричных формулах по аналогии с общим пространственным случаем сохранены обозначения матриц SF и SM, используемых при формировании бивекторов сил и пар сил. 
