







|
|
|
|
|
||
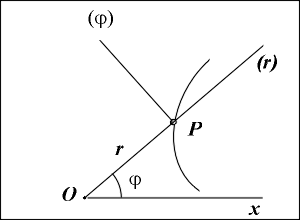
Рассмотрим, как вычисляются скорость и ускорение точки при задании ее движения в полярных координатах, то есть когда заданы уравнения движения точки в виде r = r(t); ![]() =
= ![]() (t).
(t).
В этом случае векторы v и a определяются по их проекциям на взаимно перпендикулярные подвижные оси Pr![]() , имеющие начало в точке Р и движущиеся вместе с нею (см.рис.). Эти оси направлены следующим образом:
, имеющие начало в точке Р и движущиеся вместе с нею (см.рис.). Эти оси направлены следующим образом:
Определение скорости точки
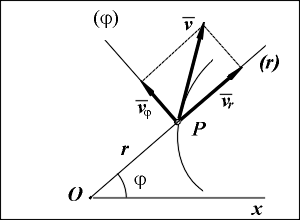
Вектор скорости v точки направлен по касательной к траектории и определяется своими проекциями vr и ![]() на оси Pr и P
на оси Pr и P![]() по формулам:
по формулам:
vr = dr/dt = ![]() ;
;
![]() = r(d
= r(d![]() /dt) = r
/dt) = r![]() .
.
В зависимости от знаков производных ![]() и
и ![]() радиальная и трансверсальная скорости могут быть как положительными, так и отрицательными (на рисунке показан случай, когда обе эти скорости положительные).
радиальная и трансверсальная скорости могут быть как положительными, так и отрицательными (на рисунке показан случай, когда обе эти скорости положительные).
Определение ускорения точки
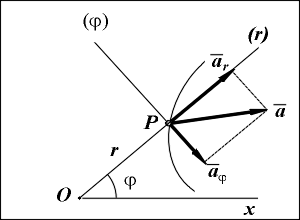
Вектор ускорения a точки направлен в сторону вогнутости траектории и определяется своими проекциями ar и ![]() на оси Pr и P
на оси Pr и P![]() по формулам:
по формулам:
ar = d2r/dt2 - r (d![]() /dt)2 =
/dt)2 = ![]() - r (
- r (![]() )2;
)2;
![]() = r (d2
= r (d2![]() /dt2) + 2 (dr/dt) (d
/dt2) + 2 (dr/dt) (d![]() /dt) = r
/dt) = r![]() + 2
+ 2 ![]()
![]() .
.
Радиальное и трансверсальное ускорения могут быть как положительными, так и отрицательными (на рисунке показан случай, когда радиальное ускорение положительное, а трансверсальное - отрицательное).
Модуль ускорения a = ( ar2 +