Приведение плоской системы параллельных сил к центру

Метод определения равнодействующей плоской системы параллельных сил

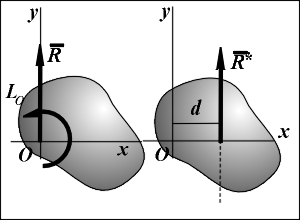
Для плоской системы параллельных сил введем координатную систему Oxy, ось Oy которой направлена параллельно линиям действия сил. Тогда проекции главного вектора R на оси координатной системы Oxy и алгебраический главный момент L_O относительно центра О определяются по формулам:

R_x = F_ix = 0; R_y = F_iy; L_O = M_O(F_i).

Если для данной системы сил главный вектор R 0, то эта система сил приводится к равнодействующей силе. При этом возможны два случая:

1. L_O = 0. В этом случае система сразу приводится к равнодействующей R, проходящей через центр О.
   
2. L_O 0. В этом случае система сил заменяется равнодействующей R^* = R, линия действия которой образуется параллельным переносом (см. рис.) линии действия силы R на расстояние d = |L_O|/R, где R - модуль главного вектора R. При этом момент силы R^* относительно точки О должен совпадать с моментом L_O по величине и знаку.
   Равнодействующая сила R^* может быть приложена к любой точке твердого тела, лежащей на этой прямой.

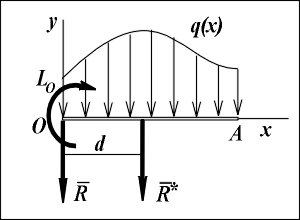
Рассмотрим теперь плоскую систему параллельных сил, распределенных по произвольному закону q(x) вдоль отрезка ОА длиной a и направленных перпендикулярно этому отрезку.

Проекции главного вектора R и алгебраический главный момент L_O относительно точки О определяются интегрированием по х в пределах от 0 до A следующих функций:

R_x = 0; R_y = q(x) dx; L_O = q(x) · x dx;

В этих формулах R_y и L_O получаются с "правильными" знаками, если интенсивность q сопровождается знаком по следующему правилу: q > 0, если распределенные силы действуют в положительном направлении оси Oy, иначе q < 0 (этот случай показан на рисунке).

Равнодействующую данной системы сил получем как вектор R^* = R, линия действия которого смещена параллельным переносом (см. рис.) линии действия силы R на расстояние d = |L_O|/R, где R - модуль главного вектора R. При этом момент силы R^* относительно точки О должен совпадать с моментом L_O по величине и знаку.

Примеры плоских систем параллельных распределенных сил и их равнодействующих