Предыдущий уровень изложения текущего раздела   Текущий уровень изложения предыдущего раздела   Текущий уровень изложения следующего раздела   Первый уровень изложения следующего раздела   Уровень:


Приведение плоской системы параллельных сил к центру

Приведем примеры замены плоских систем параллельных распределенных сил их равнодействующими.

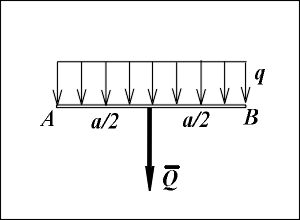  1. Силы, равномерно распределенные вдоль отрезка прямой.

    Для такой системы сил интенсивность имеет постоянное значение: q = const.

    При решении задач статики эту систему сил можно заменять сосредоточенной равнодействующей силой Q, равной по модулю произведению интенсивности q на длину отрезка AB = a ( Q = q · a) и приложенной в середине отрезка AB.





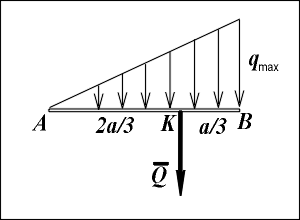  2. Силы, распределенные вдоль отрезка прямой по линейному закону.

    Для такой системы сил интенсивность q является переменной величиной, изменяющейся от нуля до максимального значения qmax по линейному закону.

    Равнодействующая Q этой системы сил равна по модулю Q =0.5 · a · qmax и приложена в точке K, делящей отрезок AB в отношении AK : KB = 2 : 1.