Приведение плоской системы сил к центру

Метод определения равнодействующей плоской системы сил

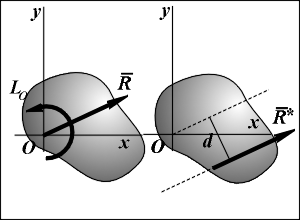
Для плоской системы сил проекции главного вектора R на оси координатной системы Oxy и алгебраический главный момент L_O относительно центра О определяются по формулам:

R_x = 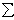F_ix; R_y = 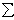F_iy; L_O = 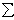M_O(F_i).

Если для данной системы сил главный вектор R 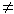0, то эта система сил приводится к равнодействующей силе. При этом возможны два случая:

1. L_O = 0. В этом случае система сразу приводится к равнодействующей R, проходящей через центр О.
   Пример
2. L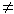_O 0. В этом случае система сил заменяется равнодействующей R^* = R, линия действия которой образуется параллельным переносом (см. рис.) линии действия силы R на расстояние d = |L_O|/R, где R - модуль главного вектора R. При этом момент силы R^* относительно точки О должен совпадать с моментом L_O по величине и знаку.
   Уравнение линии действия равнодействующей R^* имеет следующий вид:
   A·x + B·y + C = 0, где A = -R_y; B = R_x; C = L_O.
   Равнодействующая сила R^* может быть приложена к любой точке твердого тела, лежащей на этой прямой.
   Пример