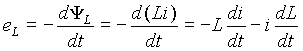 .
.
(2)
Магнитное поле вокруг отдельного проводника создается протекающим по нему током. Следовательно, и полный магнитный поток
Y L будет связан с собственным током проводника i|
Y L=Li. |
(1) |
Коэффициент
L , связывающий между собой ток и потокосцепление, называется коэффициентом самоиндукции или индуктивностью цепи. Очевидно, что он зависит от геометрической формы и размеров цепи, а также от свойств среды, в которой она находится, т.е. L=F(g1, g2,...gn, m ) , где gk - это некоторые геометрические параметры, а m - магнитная проницаемость.Индуктивность измеряется в
генри (Гн=Вб/А).Индуктивность цепи принципиально является положительной величиной L>0, а при постоянных геометрических параметрах и магнитной проницаемости она представляет собой некую константу. Кроме того, она не может быть равной нулю, т.к. это означало бы отсутствие магнитного поля вокруг проводника с током. Ее можно только уменьшить, например, максимальным сближением проводников с одинаковым током протекающим в противоположных направлениях.
Любое изменение
Y L по закону электромагнитной индукции должно приводить к появлению ЭДС|
|
(2) |
Электродвижущая сила
eL называется ЭДС самоиндукции, т.к. наводится (индуктируется) собственным магнитным потоком или потоком самоиндукции Y L проводника.Из выражения (2) следует, что ЭДС самоиндукции может возникать как при изменении тока в проводнике, так и при изменении индуктивности, т.е. геометрических параметров цепи и свойств среды.
В случае, если
L=const выражение (2) упрощается|
|
(3) |
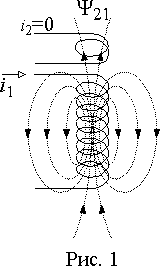
Если вблизи проводника или катушки с током расположить другой проводник или катушку, то часть магнитного потока первой катушки
Y 21 будет сцепляться со второй (рис. 1). Величина этого потока определяется геометрическими параметрами второй катушки, ее расположением относительно первой, а также магнитными свойствами окружающей среды, т.е. Y 21 = M21i1. В этом выражении коэффициент M21 называется коэффициентом взаимной индукции или взаимной индуктивностью и по смыслу аналогичен индуктивности L .Коэффициент взаимной индукции, также как индуктивность, измеряется в генри.
При изменении потока взаимной индукции
Y 21 во второй катушке будет наводиться ЭДС взаимной индукции|
|
(4) |
Если принять, что в первой катушке ток отсутствует, а протекает во второй, то вторая катушка создаст поток взаимной индукции
Y 12 = M12i2, связанный с ее током, и изменение этого потока будет наводить в первой катушке ЭДС|
|
(5) |
Взаимные индуктивности
M12 и M21 всегда равны и в них можно опустить индексы :|
|
(6) |
В общем случае наличия токов в обеих катушках потоки взаимной индукции могут по разному ориентироваться по отношению к собственным потокам катушек. Если обозначить полное потокосцепление первой катушки через
Y 1F, то его можно представить тремя слагаемыми|
Y 1F = Y 11+ Y 12± Y 21 = Y 1 ± Y 21 =L1i1 ± Mi2 , |
(7) |
Аналогично для второй катушки
|
Y 2F = Y 22+ Y 21± Y 12 = Y 2 ± Y 12 =L2i2 ± Mi1. |
(8) |
По закону электромагнитной индукции определим ЭДС первой и второй катушек с помощью выражений (7) и (8)
|
|
(9) |
Таким образом, в каждой катушке магнитный поток наводит ЭДС, имеющие две составляющие. Первая связана с той частью потока, которая создается собственным током катушки. Эта часть ЭДС всегда положительна и называется ЭДС самоиндукции. Вторая часть ЭДС называется ЭДС взаимной индукции .Она наводится той частью магнитного потока, которая создается другой катушкой. ЭДС взаимной индукции может быть положительной или отрицательной в зависимости от взаимной ориентации магнитных потоков обеих катушек. Соответственно положительной или отрицательной может быть взаимная индуктивность
M . Значение M считают положительным, если при произвольно выбранных положительных направлениях токов в катушках потоки взаимной индуктивности совпадают по направлению с потоками самоиндукции.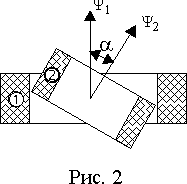
Значение M может быть также переменным, например, в системе из двух цилиндрических катушек, одна из которых может поворачиваться относительно оси, расположенной в плоскости другой (рис. 2). Такие катушки называются вариометром. В этом случае взаимная индуктивность изменяется в функции угла a между нормалями к плоскостям катушек
M = Mmaxcosa
и принимает любые значения в пределах от -
Mmax до +Mmax. Максимальное значение M соответствует совпадению направлений нормалей, а при повороте на ± 90° взаимная индуктивность становится равной нулю. В режиме непрерывного вращения a = w t и взаимная индуктивность становится гармонической функцией времени M = Mmaxcosw t.Если вторую катушку на
рис. 1 замкнуть накоротко, то в ней будет протекать ток i2 под действием ЭДС взаимной индукции. Положим равными нулю сопротивления обеих катушек. Тогда в контуре второй катушки ЭДС взаимной индукции будет уравновешиваться ЭДС самоиндукции, т.е. e2L+ e2M = 0.|
|
(10) |
В контуре первой катушки ЭДС источника питания
e1 уравновешивает обе составляющие ЭДС индукции|
|
(11) |
Индуктивность
L'1 всегда положительна, поэтому|
|
(12) |
Отношение
|
|
(13) |
называется коэффициентом связи двух цепей. Его значение всегда положительно и меньше единицы. Теоретически он может быть равным единице, но это возможно только при полном слиянии двух катушек, при котором они перестают существовать как отдельные цепи. Положительное значение
k во втором равенстве выражения (13) на первый взгляд противоречит возможности отрицательных значений M . Однако это кажущееся противоречие, возникающее при формальном преобразовании числителя, и несуществующее в первом равенстве.То, что коэффициент связи всегда меньше единицы легко доказать, пользуясь выражениями
(7) и (8). Из них следует, что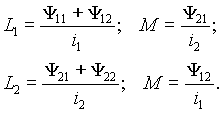
Подставим эти значения в выражение (13)
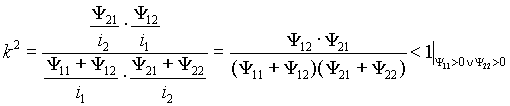 ,
,
что и подтверждает принятое ранее условие
k<1.Из выражения (13) следует, что должно соблюдаться соотношение
|M|<L1<L2 или L1<|M|<L2, т.е. взаимная индуктивность может быть либо меньше индуктивностей обеих катушек, либо меньше одной из них. Второе условие означает, что при значительной разнице числа витком катушек w1<<w2 поток взаимной индукции может оказаться больше потока самоиндукции катушки с меньшим числом витков.