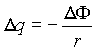При анализе магнитного поля ранее было установлено, что приращение количества зарядов D q , протекающих через замкнутый электрический контур в течение некоторого времени, пропорционально приращению пронизывающего этот контур магнитного потока D Ф в течение того же времени, взятому с обратным знаком.

где r - сопротивление контура.

но из определения электрического тока, как количества электрических зарядов перемещающихся через поперечное сечение проводника в единицу времени i=dq/dt , следует, что dq=idt . Отсюда

Произведение ir представляет собой падение напряжения в контуре электрической цепи, пронизываемом магнитным потоком Ф, и по второму закону Кирхгофа оно должно уравновешиваться ЭДС, действующей в этом контуре. Следовательно, величина, стоящая в правой части выражения (3), является электродвижущей силой, под действием которой в контуре протекает электрический ток i или

Таким образом явление электромагнитной индукции заключается в появлении (наведении) в проводящем контуре, находящемся в магнитном поле, электродвижущей силы в случае изменения величины магнитного потока, проходящего через поверхность, ограниченную этим контуром.

Выражение (4) представляет собой одну из математических записей закона электромагнитной индукции - ЭДС, наводимая в контуре электрической цепи, равна взятой с обратным знаком скорости изменения магнитного потока, проходящего через поверхность, ограниченную этим контуром.

Строго говоря, условие проводимости контура, в котором наводится ЭДС не является необходимым. ЭДС будет наводиться и в непроводящем контуре, т.е. в диэлектрике. Различие для проводящего и непроводящего контуров будет заключаться лишь в том, что в проводящем контуре при замыкании его будет протекать ток проводимости, а в непроводящем - ток смещения.

Если от рассмотрения контура одного витка перейти к катушке, состоящей из некоторого количества витков, то величину магнитного потока во всех выражениях нужно заменить потокосцеплением Y . Тогда ЭДС, наводимая в катушке будет

Формулировка закона электромагнитной индукции, соответствующая выражению (4), относится только к контурам ограничивающим некоторую поверхность и впервые была дана Максвеллом. Однако ЭДС может наводиться и на отдельных участках контура. Это очевидно, если представить магнитный поток Ф числом единичных магнитных трубок или соответствующих линий N, т.е. Ф = N или D Ф = D N и dФ = dN . Отсюда

Так как трубки магнитного потока непрерывны, то их число может измениться только, если они пересекут поверхность образованную контуром. Следовательно, ЭДС, наводимая в контуре электрической цепи, равна взятой с обратным знаком скорости пересечения контура магнитными линиями.

Такая формулировка соответствует формулировке закона электромагнитной индукции Фарадея. Очевидно, что для контуров, ограничивающих поверхность, обе формулировке тождественны. Однако, магнитные линии могут пересекать не только контур, но и проводник, и в этом случае выражение (6) позволяет определить индуктированную ЭДС.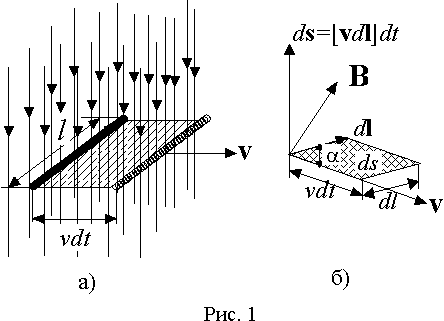

Пусть, например, прямой отрезок проводника длиной l перемещается в однородном магнитном поле перпендикулярно линиям индукции в направлении перпендикулярном его оси со скоростью v (рис. 1 а)). В течение времени dt он переместится на расстояние vdt и опишет поверхность площадью lv dt . Так как число единичных магнитных линий, проходящих через нормальную поверхность численно равно магнитной индукции B, то число линий dN, которые пересечет проводник за время dt будет равно Blv dt. Отсюда абсолютное значение ЭДС

e = Blv.

В общем случае проводника произвольной формы и ориентации в пространстве, движущегося в неоднородном магнитном поле, можно написать выражение для элементарной ЭДС de , индуктируемой в элементарном отрезке проводника dl. Если dl - вектор, направленный по оси элементарного проводника (рис. 1 б)), а v - вектор скорости, направленный под уголом a к dl , то поверхность, описываемая элементарным проводником за время dt будет равной ds=vdlsina dt , т.е. ее можно представить векторным произведением ds=[vЧ dl]dt . Элементарный магнитный поток через эту поверхность равен dФ=Bds=B[vЧ dl]dt. Отсюда элементарная ЭДС, наводимая в отрезке dl

ЗАДАЧА 1

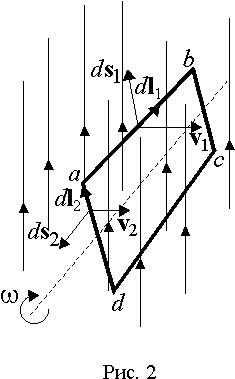
Рассмотрим имеющий большое практическое значение частный случай индукции ЭДС в прямоугольной рамке abcd, вращающейся в однородном магнитном поле с угловой частотой w относительно оси перпендикулярной направлению магнитного потока (рис. 2).

Выделим на сторонах ab и da элементарные отрезки dl₁ и dl₂. Вектора скорости движения этих отрезков v₁ и v₂ в любой момент времени направлены перпендикулярно плоскости рамки. Поэтому вектора элементарных поверхностей ds₁ и ds₂, описываемых элементарными отрезками dl₁и dl₂, будут располагаться в плоскости рамки перпендикулярно сторонам ab и da. Следовательно, для второго элементарного отрезка угол между векторами B и ds₂ будет постоянного равен 90° и поток вектора индукции через эту поверхность равен нулю. Отсюда будет равна нулю и ЭДС наводимая в любом элементарном отрезке сторон da и bc вращающейся рамки.

Раскроем выражение (7) для элементарного отрезка dl₂ в виде de=Bcosb (dl₂vsina ), где b =w t - угол между вектором и нормалью к поверхности ds₂, а a = 90° - угол между векторами v и dl₂. Отсюда de=BЧ cosw tЧ dl_{2 Ч} v, но модуль скорости движения равен v = w bc/2. Таким образом, ЭДС, наводимая в стороне ab рамки равна

где s = abЧ bc - площадь рамки, представленная через размеры ее сторон.

Очевидно, что если распространить интегрирование на другую сторону рамки bc, то ЭДС будет вдвое больше, т.е. e_abcd=w BsЧ cosw t .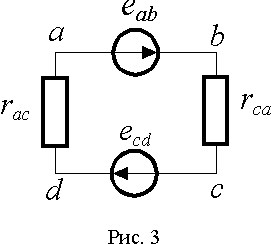

Таким образом, вращающуюся в магнитном поле рамку можно представить в виде электрической цепи с двумя источниками ЭДС, наводимыми в сторонах ab и cd рамки. Эти стороны называются активными сторонами и играют большую роль в процессах преобразования энергии в электрических машинах. Две другие стороны рамки создают электрическую связь для протекания тока в контуре рамки.

Ф = Bscos(90° - b ) = Bscos(90° - w t)= Bssinw t.

В этом выражении косинус угла между вектором индукции и нормалью к плоскости рамки представлен через угол b между вектором индукции и плоскостью рамки. Отсюда ЭДС индуктируемая в рамке при вращении

Таким образом, мы получили тождественные выражения для результирующей ЭДС, пользуясь различными представлениями закона электромагнитной индукции. Эти результаты можно обобщить, пользуясь понятием потокосцепления, для рамки с числом витков w .

ЗАДАЧА 2