Опр. 1
Опр. 2
Опр. 3
Опр. 4
Опр. 5
Опр. 6
6.5.1. Линейный оператор
Оператором называется отображение
![]()
![]()
где ![]() -некоторые
пространства (мы будем обычно рассматривать гильбертовы пространства).
-некоторые
пространства (мы будем обычно рассматривать гильбертовы пространства).
Область определения оператора ![]() -
множество, на котором задано действие оператора,
область значений оператора
-
множество, на котором задано действие оператора,
область значений оператора ![]() .
.
Обычно мы будем иметь дело со случаем H=G.
Операторы ![]() называются равными, если:
называются равными, если:
![]()
![]()
Оператор ![]() называется расширением А,
а А – сужением
называется расширением А,
а А – сужением ![]() (обозначается
(обозначается ![]() ),
если:
),
если:
![]()

Оператор А называется непрерывным
в точке ![]() если
для всякого
если
для всякого ![]() найдется такое
найдется такое ![]() ,
что
,
что ![]() если
если ![]()
Оператор А называется непрерывным, если он непрерывен в каждой точке D(A).
Линейный оператор –это многомерный аналог
функции одной переменной, графиком которой служит прямая, проходящая через
начало координат, то есть функций ![]() для некоторого
для некоторого ![]() .
.
Оператор L с областью определения
D(L) называется линейным, если для всех ![]() и всех
и всех ![]() :
:
![]()
![]() .
.
Многие и весьма разнообразные уравнения представимы в виде
![]()
![]()
где L – линейный оператор.
Рассмотрим примеры линейных операторов.
Примеры.
1. Один из простейших примеров линейного оператора в функциональном пространстве является умножение на заданную функциюесть оператор А определен требованием, чтобы
![]()
![]()
Если ![]() непрерывна,
то
непрерывна,
то
![]()
![]()
![]()
![]() ,
,
где ![]()
Для того чтобы левая часть имела смысл,
f должна быть достаточно гладкой. Поскольку g непрерывна,
естественно взять в качестве области определения искомого оператора ![]() и задать
и задать ![]() в этой области соотношением
в этой области соотношением
![]()
![]()
При этом функция Af будет непрерывной и не обязательно дифференцируемой. Поэтому
![]() а уравнение примет вид
а уравнение примет вид ![]() .
.
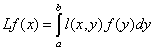 .
.
При этом ![]() будет непрерывной функцией и L- линейный оператор из
будет непрерывной функцией и L- линейный оператор из ![]() в себя. Функция
в себя. Функция ![]() называется
ядром интегрального оператора L.
называется
ядром интегрального оператора L.