5.4. Уравнение теплопроводности в трехмерном пространстве
Оператор Лапласа в 3-х-мерном пространстве.
-
оператор Лапласа в трехмерном пространстве.
 . |
(1) |
.
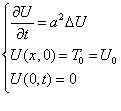Теперь можно решить эту задачу,
учитывая, что Земля является шарообразной. Будем искать сферически симметричные
решения уравнения теплопроводности, то есть полагаем, что U не
зависит от 
и от
,
,
тога два последних слагаемых в уравнении (1) равны 0.
,
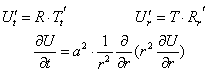
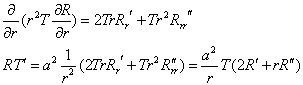
где 
пусть 
 . |
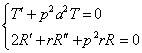(2) (3) |
-
решение уравнения (2).
Для того чтобы решить уравнение (3) необходимо сделать замену переменной.
Пусть 
,
Найдем первую и вторую производные R(r).
.
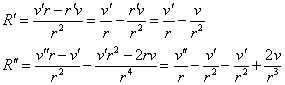Подставим полученные выражения в уравнение (3):
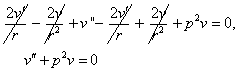
Найдем корни характеристического уравнения:
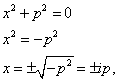
тогда
.
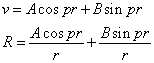Функция U(r,t) должна быть ограничена внутри шара.
-
краевое условие.
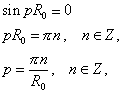
Пользуясь линейностью уравнения, решение будем искать в виде ряда
 . |
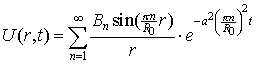(4) |
Удовлетворим начальным условиям:
.
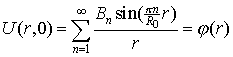Значит 
-это
коэффициенты в разложении функции 
в ряд Фурье по синусам.
.
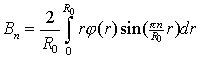Подстановка найденных коэффициентов
в формулу (4) дает решение
задачи.