Доказательство теоремы единственности для уравнения колебаний струны.
Пусть есть 2 решения 
Рассмотрим
разность 
.Функция
V(x,t) удовлетворяет однородному уравнению и однородным дополнительным
условиям
  |
(4) |
Следовательно, если решений два, то их разность
должна удовлетворять однородной краевой задаче (4). Таким образом, надо
доказать, что у однородной задачи только нулевое решение
( т.е. нетривиальных решений нет ).
Физически, теорема единственности доказывается из закона сохранения энергии :
 |
-полная энергия струны в момент времени t, |
Докажем, что E от tне
зависит, т. е. функция 
.
Для этого надо доказать, чтоE(t)=0. Продифференцируем
E(t) по t выполняя при этом дифференцирование под
знаком интеграла.
Проинтегрируем по частям:
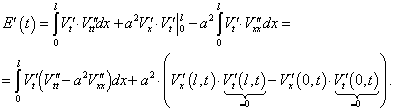
Подстановка обращается в нуль в силу граничных
условий. Из 
следует
и аналогично для x=l. Получаем
 |
(5) |
,
тогда
Таким образом, доказали, что :
.
Учитывая начальные условия, получаем:
это значит, что при любом t:
 , |
(6) |
| так как |  |
Пользуясь формулой (6) заключаем, что
откуда и следует, что
Пользуясь начальным условием, находим:
тем самым доказано, что
Следовательно, если существуют две функции
,
удовлетворяющие всем условиям теоремы,
то 
Теорема доказана.