1.4.2. Неоднородное уравнение струны (вынужденные колебания струны)

Найти решение неоднородного уравнения

,

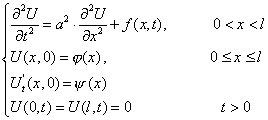(1)

где заданная функция.

Эти вынужденные колебания общего типа можно представить себе как результат сложения двух колебательных движений, из которых одно есть чисто вынужденное колебание, то есть такое, которое совершается по действием силы, причем струна в начальный момент не выведена из состояния покоя, другое есть свободное колебание, которое струна совершает без действия силы, только вследствие начального возмущения. Аналитически это приводит к введению вместо U двух новых функций V и W.
Ищем решение в виде суммы двух функций U(x,t)=V(x,t)+W(x,t) одна из которых удовлетворяет однородному уравнению и неоднородным начальным условиям, например, функция , решение которого мы рассмотрели в разделе 1.4.1, а вторая удовлетворяет неоднородному уравнению и однородным начальным условиям.

.

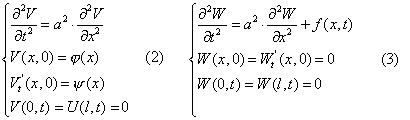Рассмотрим систему (3). и разложим в ряд по синусам.

Разложим функцию f(x,t) в ряд Фурье по синусам на отрезке :

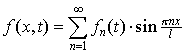,	(4)
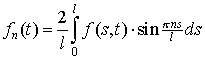,	(5)

,

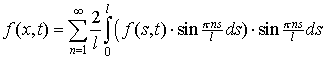Как и в случае свободных колебаний, мы будем искать функцию W в виде ряда:

.

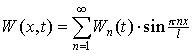(6)

Решим уравнение системы (3). Для этого найдем производные:

,

,

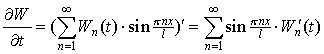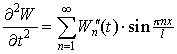(7)

,

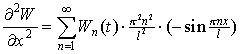(8)

Подставим выражения (4), (7), (8) в уравнение (3) и решим его.

.

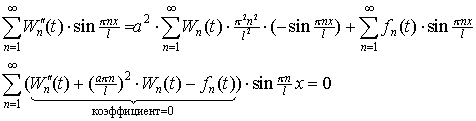
(9)

Необходимо удовлетворить начальным условиям:

.

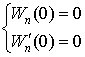(10)

Для определения мы получили обукновенное дифференциальное уравнение с постоянными коэффициентами. Начальные условия дают:

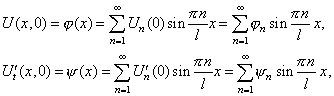
откуда следует:

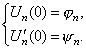
Эти дополнительные условия полностью определяют решение уравнения (9).

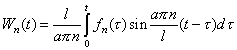-решение неоднородного уравнения с нулевыми начальными условиями и

- решение однородного уравнения с заданными начальными условиями. Таким образом, искомое решение запишется в виде

.
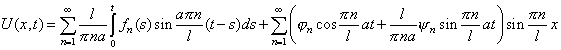