2.3 Теорема Ван Циттерта – Цернике. Значение теоремы и следствия из нее.

Эта теорема является одной из наиболее важных теорем современной оптики. Она описывает преобразование поперечной корреляционной функции светового пучка в процессе распространения. В соответствии с этой теоремой оказывается, что поперечный радиус корреляции частично когерентного волнового пучка в процессе распространения за счет дифракции увеличивается.

Будем считать, что свет является квазимонохроматическим. Мы знаем, что взаимная интенсивность распространяется в соответствии с законом

,

который справедлив для различной степени когерентности, характеризуемой взаимной интенсивностью J(P₁,P₂).

Для некогерентного источника с точностью до константы

.

Взаимная интенсивность получается, используя "избирательные" свойства d - функции.

.

Чтобы упростить это выражение, примем некоторые предположения и приближения.

1.Размеры источника и области наблюдения намного меньше расстояния z, от источника до плоскости наблюдения, тогда

.

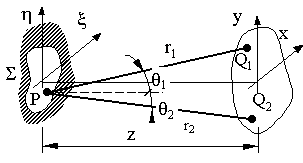
Рис.9. К выводу теоремы Ван Циттерта-Цернике

Тогда выражение для взаимной интенсивности в наблюдаемой области .

Далее, предполагая, что плоскости источника излучения и наблюдения параллельны и учитывая параксиальное приближение

Вводя обозначения  и, принимая во внимание, что I(x,h) = 0 для области вне источника S, окончательно получим

,

где фазовый множитель

;

r₁ и r₂ - расстояния от точек (x₁,y₁) и (x₁,y₂) до оптической оси.

В нормированном виде теорема принимает вид

.

Если выполняется равенство, то

- есть видность.

Значение теоремы и следствия из нее. Теорема Ван Циттерта-Цернике, может быть сформулирована следующим образом: с точностью до множителя exp(-jY) и масштабных постоянных взаимную интенсивность J(x₁,y₁;x₂,y₂) можно найти, выполнив двумерное преобразование Фурье распределения интенсивности I(x,h) по поверхности источника.

Следует также обратить внимание, что ½g½зависит только от разности координат (Dx, Dy).

Поскольку множитель exp(-jy) может быть опущен в случаях:

1. то  y < p/2 и exp(-jy) » 1.

2.Если точки Q₁ и Q₂ находятся на одинаковом расстоянии от оптической оси то фаза y = 0.

3.Если отверстия лежат не на плоскости, а на сфере радиусом z с центром на источнике.

ПРИМЕР: Круглое отверстие. Пусть источник представляет собой круг с радиусом a. В соответствии с теоремой Ван Циттерта-Цернике функция комплексной когерентности описывается функцией Эйри. Эта зависимость показана на рис. 10.

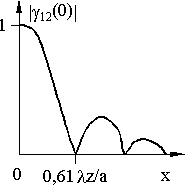
Рис.10. Функция комплексной когерентности для круглого источника

Первый нуль модуля |g₁₂| имеет место при 0.61lz/a. Следовательно, колебания в точках (x₁,y₁) и (x₂,y₂) полностью некогерентны при удалении их друг от друга на расстояние d, равное 0,61lz / a. Если считать допустимой степень частичной когерентности между точками равной 0.88, то необходимо, чтобы расстояние d между ними удовлетворяло условию

a - угол, под которым виден радиус источника.

Расстояние между точками, для которых |g₁₂| = 0.88 называется интервалом пространственной когерентности.

---