1 ПРОСТРАНСТВЕННАЯ КОГЕРЕНТНОСТЬ

ИЗЛУЧЕНИЯ ЛАЗЕРА

1.1 Одно- и многомодовый режим излучения лазера. Радиус корреляции лазерного излучения

Поперечная структура реальных лазерных пучков имеет случайный характер, что обусловлено целым рядом естественных причин: спонтанные шумы, статистика многих поперечных мод.

Рис.1. Причины случайного характера поперечной структуры реальных лазерных пучков

Чем же определяются характерные масштабы поперечных корреляций лазерного излучения?

Предположим, что возбуждаемые в лазере моды с различными поперечными индексами m и n вырождены по частоте, тогда многомодовое излучение можно записать следующим образом

,

где A_m,n  и j_m,n - не зависящие от времени комплексные амплитуды и фазы мод, z - координата вдоль направления распространения пучка, отсчитываемая от области перетяжки.

Распределение амплитуд A_m,n зависит от типа оптического резонатора и формы зеркал. Наиболее простой вид распределения амплитуды A_m,n имеют для плоского резонатора (случай прямоугольных зеркал)

,

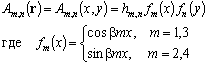где b, комплексный параметр, зависящий от базы резонатора и апертуры зеркал.

Aналогичный вид имеет функция f_n(y).

Для пространственной поперечной корреляционной функции на выходе резонатора по определению имеем:

.

В случае статистически независимых фаз j_m,n поперечных мод

.

Рассчитаем корреляционную функцию вблизи центра пучка (r = 0), смещение s зададим вдоль оси x и будем считать, что возбуждаются поперечные моды с индексами от m = 1 до .

Пусть нечетно и коэффициенты h_m,n - одинаковы, тогда для пространственной поперечной корреляционной функции получим

.

При большом числе поперечных мод N >> 1, модуль степени пространственной когерентности равен

.

Модуль степени пространственной когерентности является квазипериодической функцией. В реальных случаях база резонатора много больше радиуса зеркал (L >> a), а число Френеля С учетом этого условия, радиус корреляции .

Таким образом, для многомодовых лазерных пучков, возбуждаемых в плоскопараллельном резонаторе с прямоугольными зеркалами радиус корреляции обратно пропорционален числу возбуждаемых поперечных мод .

Но это соотношение можно использовать лишь для грубых оценок. Отличия от эксперимента могут быть связаны с неоднородностями активной среды, неравномерностью распределения интенсивностей по модам.

Приближенный расчет радиуса корреляции лазерного поля со статистически независимыми модами можно выполнить, оценивая средний размер неоднородности по возбуждаемым модам, который в соответствии с выражением для распределения амплитуды моды по половинному уровню можно оценить как r_m » 2a ¤ m.

Для плоского резонатора получим .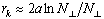

Таким образом, данное выражение, которое получается исходя из поперечной неоднородности лазерного пучка, дает практически такую же зависимость, что и предыдущее.

При наличии неоднородностей внутри резонатора даже для плоского резонатора более адекватной оказывается модель сферического резонатора.

Аналогичным способом, исходя из масштаба радиальных неоднородностей, можно найти радиус корреляции для сферического резонатора .

Последнее выражение существенно отличается от выражения, полученного для плоского резонатора, т.к. в последнем случае с увеличением номера радиального индекса поперечной моды n размер поперечных осцилляций становится обратно пропорциональным , где n радиальный индекс полинома Лагерра, определяющий число радиальных осцилляций в моде сферического резонатора.

Рис.2. Зависимость радиуса поперечной корреляции от формы резонатора

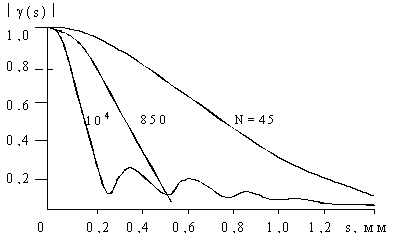
Рис.3. Вид поперечной корреляционной функции излучения твердотельного многомодового лазера. N – число мод

Зависимость радиуса корреляции от числа поперечных мод хорошо подтверждается экспериментально.

Радиус корреляции лазерного пучка, как и ширина пучка, является функцией продольной координаты z. Измерения показали, что для многомодового режима при удалении от выходного зеркала отношение диаметра пучка к радиусу корреляции сохраняется постоянным:

Рис.4. Значение радиуса корреляции в различных точках поперечного сечения многомодового лазерного пучка.

, что следует из характера изменения масштаба неоднородностей поля. Оно пропорционально . Поведение пространственной корреляционной функции излучения многомодового лазера, с изменением числа генерируемых поперечных мод, хорошо согласуется с представлениями, основанными на описании поперечного распределения лазерного поля, как результата наложения статистически независимых поперечных мод. Для точного расчета формы поперечных корреляционных функций необходимо располагать информацией об амплитудах мод, возбуждаемых в лазере. Следует отметить, что при большом числе поперечных мод, корреляционная функция поля близка по виду к корреляционной функции однородного d-коррелированного шума, профильтрованного через круглую диафрагму.

---