ОБЩЕТЕОРЕТИЧЕСКИЕ

ПОЛОЖЕНИЯ

Когерентность излучения. Понятие когерентности в оптике вводится для характеристики согласованности (корреляции) световых колебаний в различных точках пространства и в различные моменты времени. Определим степень когерентности посредством корреляционной функции светового поля. Рассмотрим поляризованное поле, вектор напряженности электрического поля E которого колеблется в определенном направлении. Если вектор напряженности содержит компоненту, случайным образом изменяющуюся по пространственным координатам r и по времени 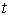, то можно построить следующую корреляционную функцию

,

где угловые скобки означают усреднение по всему пространству и по всему интервалу времени наблюдения. Для стационарных полей, статистические характеристики которых во времени не меняются,

.

Принято выделять также статистически однородные поля, для которых корреляционная функция зависит лишь от разности r₂ - r₁

.

Однородное случайное поле называется изотропным, если корреляционная функция зависит лишь от абсолютного значения расстояния между двумя точками . Для стационарных во времени и однородных в пространстве случайных полей

,

где . Корреляционная функция принимает максимальное значение при .

Введем применительно к световому пучку нормированную корреляционную функцию

где - значение интенсивности пучка в указанных пространственных точках и в указанные моменты времени. В случае стационарности поля светового пучка

Построенную таким образом величину называют комплексной степенью когерентности, так как корреляционные функции в общем случае комплексны. Абсолютную величину называют модулем степени когерентности или просто степенью когерентности. Степень когерентности всегда удовлетворяет неравенству

при дает значение степени пространственной когерентности, а при - значение степени временной когерентности. Значение и , при которых степень пространственной и временной когерентности уменьшаются в заданное число раз называются соответственно размером зоны когерентности и временем когерентности.

---